Next: Integral of Gaussian Up: Derivations and Computations Previous: Fourier Series * Contents
To allow wave functions to extend to infinity, we will expand the interval used
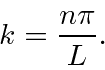
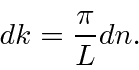
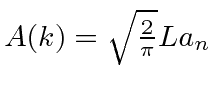 , we can make the transform come out with the constants we want.
, we can make the transform come out with the constants we want.
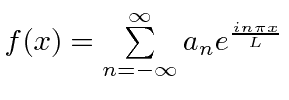 |
Standard Fourier Series |
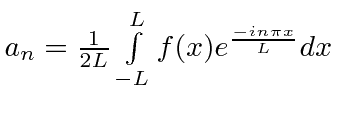 |
Standard Fourier Series |
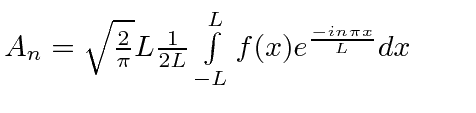 |
redefine coefficient |
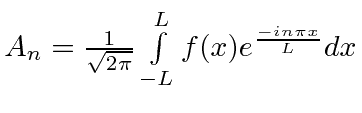 |
|
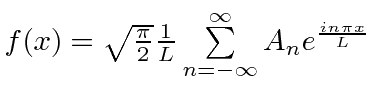 |
f stays the same |
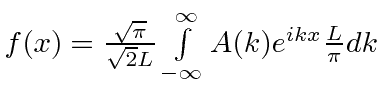 |
but is rewritten in new A and dk |
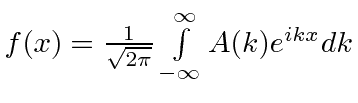 |
result |
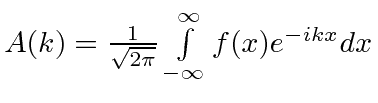 |
result |
This is just the extension of the Fourier series to all
![]() .
.
If
 is normalized, then
is normalized, then
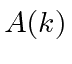 will also be normalized with this (symmetric) form of the Fourier Transform.
Thus, if
will also be normalized with this (symmetric) form of the Fourier Transform.
Thus, if
 is a probability amplitude in position-space,
is a probability amplitude in position-space,
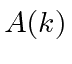 can be a probability amplitude (in k-space).
can be a probability amplitude (in k-space).
Jim Branson 2013-04-22