Probability Amplitudes

In Quantum Mechanics, we understand this wave-particle duality using (complex) probability amplitudes which satisfy a wave equation.

$$\bgroup\color{black}\psi(\vec{x},t)=e^{i(\vec{k}\cdot\vec{x}-\omega t)}=e^{i(\vec{p}\cdot\vec{x}-Et)/\hbar}\egroup$$

The probability to find a particle at a position $\vec{x}$ at some time $t$ is the absolute square of the probability amplitude $\psi(\vec{x},t)$.

$$\bgroup\color{black}P(\vec{x},t)=\left\vert\psi(\vec{x},t)\right\vert^2\egroup$$

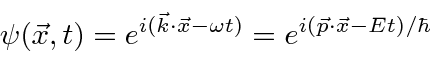
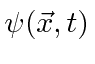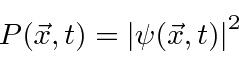
To compute the probability to find an electron at our thought experiment detector, we add the probability amplitude to get to the detector through slit 1 to the amplitude to get to the detector through slit 2 and take the absolute square.

$$\bgroup\color{black}P_{\mathrm{detector}}=\left\vert\psi_1+\psi_2\right\vert^2\egroup$$

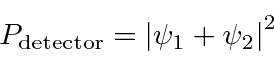
Quantum Mechanics completely changes our view of the world. Instead of a deterministic world, we now have only probabilities. We cannot even measure both the position and momentum of a particle (accurately) at the same time. Quantum Mechanics will require us to use the mathematics of operators, Fourier Transforms, vector spaces, and much more.