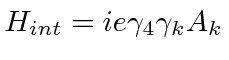The interaction Hamiltonian for the Dirac equation can be deduced in several ways.
The simplest for now is to just use the same interaction term that we had for electromagnetism
and identify the probability current multiplied by the charge (-e) as the current that couples to the EM field.
Removing the
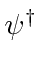 from the left and
from the left and
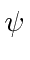 from the right and dotting into
from the right and dotting into
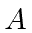 , we have the interaction Hamiltonian.
, we have the interaction Hamiltonian.
Note the difference between this interaction and the one we used in the non-relativistic case.
The relativistic interaction has just one term, is linear in
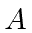 , and is naturally proportional to the coupling
, and is naturally proportional to the coupling
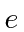 .
There is no longer an
.
There is no longer an 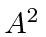 term with a different power of
term with a different power of
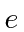 .
This will make our perturbation series also a series in powers of
.
This will make our perturbation series also a series in powers of
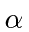 .
.
We may still assume that
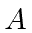 is transverse and that
is transverse and that
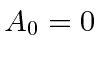 by choice of gauge.
by choice of gauge.
Jim Branson
2013-04-22
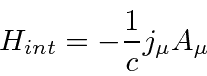
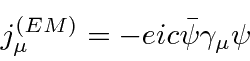
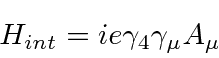
![]() is transverse and that
is transverse and that
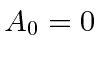 by choice of gauge.
by choice of gauge.