Next: The Relativistic Interaction Hamiltonian Up: Dirac Equation Previous: Bilinear Covariants Contents
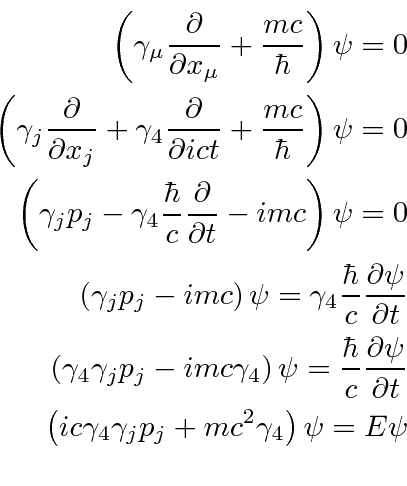
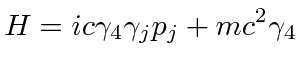 |
Its easy to see the
![]() commutes with the Hamiltonian for a free particle so that momentum will be conserved.
commutes with the Hamiltonian for a free particle so that momentum will be conserved.
The components of orbital angular momentum do not commute with
![]() .
.
![\begin{displaymath}\bgroup\color{black} [H,L_z]=ic\gamma_4[\gamma_jp_j,xp_y-yp_x]=\hbar c\gamma_4(\gamma_1p_y-\gamma_2 p_x) \egroup\end{displaymath}](img539.png)
The components of spin also do not commute with
![]() .
.
![\begin{eqnarray*}
\Sigma_z&=&{[\gamma_1,\gamma_2]\over 2i}= {\gamma_1\gamma_2\ov...
...1\gamma_2\gamma_j]
=\hbar c\gamma_4[\gamma_2p_x-\gamma_1p_y] \\
\end{eqnarray*}](img4353.png)
![\begin{displaymath}\bgroup\color{black} [H,\vec{S}\cdot\vec{p}]=[H,\vec{S}]\cdot...
...=\hbar c\gamma_4\vec{p}\times\vec{\gamma}\cdot\vec{p}=0 \egroup\end{displaymath}](img4354.png)
From the above commutators
![\bgroup\color{black}$[H,L_z]$\egroup](img4355.png) and
and
![\bgroup\color{black}$[H,S_z]$\egroup](img4356.png) , the components of total angular momentum do commute with
, the components of total angular momentum do commute with
![]() .
.
![\begin{eqnarray*}[H,J_z]=[H,L_z]+[H,S_z]=\hbar c\gamma_4(\gamma_1p_y-\gamma_2 p_x)+\hbar c\gamma_4[\gamma_2p_x-\gamma_1p_y]=0 \\
\end{eqnarray*}](img541.png)
We will need another conserved quantity for the solution to the Hydrogen atom; something akin to the
![]() in
in
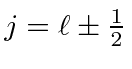 we used in the NR solution.
We can show that
we used in the NR solution.
We can show that
![\bgroup\color{black}$[H,K]=0$\egroup](img4357.png) for
for
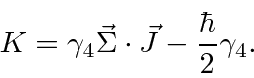
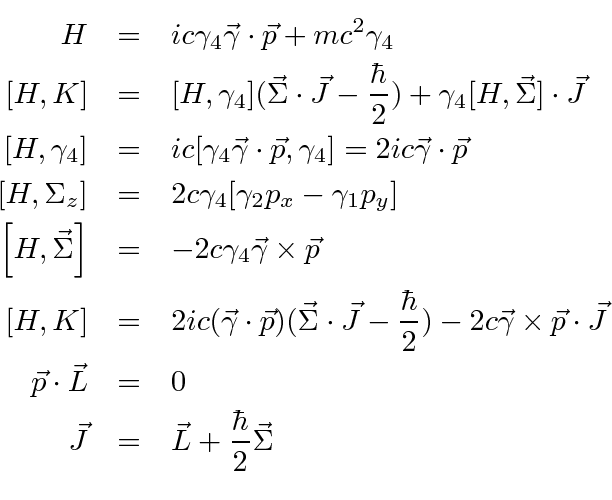
![\begin{eqnarray*}
\left[H,K\right]&=&2c\left(i(\vec{\gamma}\cdot\vec{p})(\vec{\S...
...vec{p}\cdot\vec{\gamma}-i(\vec{\gamma}\cdot\vec{p})\right)=0 \\
\end{eqnarray*}](img4360.png)
It is also useful to show that
![\bgroup\color{black}$[K,\vec{J}]=0$\egroup](img4361.png) so that we have a mutually commuting set of operators to define our eigenstates.
so that we have a mutually commuting set of operators to define our eigenstates.
![\begin{displaymath}\bgroup\color{black} [K,\vec{J}]=[\gamma_4\vec{\Sigma}\cdot\v...
...}\cdot\vec{J},\vec{J}]-{\hbar\over 2}[\gamma_4,\vec{J}] \egroup\end{displaymath}](img4362.png)
![\bgroup\color{black}$[\gamma_4,\vec{J}]=0$\egroup](img4363.png) and
and
![\bgroup\color{black}$[\vec{\Sigma}\cdot\vec{J},\vec{J}]=0$\egroup](img4364.png) .
.
![\begin{eqnarray*}
\left[\gamma_4,\vec{J}\right]&=&[\gamma_4,\vec{L}+{\hbar\over ...
...\hbar(\epsilon_{ijk}\Sigma_jL_k-\epsilon_{ijk}\Sigma_jL_k)=0 \\
\end{eqnarray*}](img4365.png)
Jim Branson 2013-04-22