Next: Bilinear Covariants Up: Dirac Equation Previous: Relativistic Covariance Contents
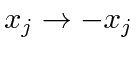 and
and
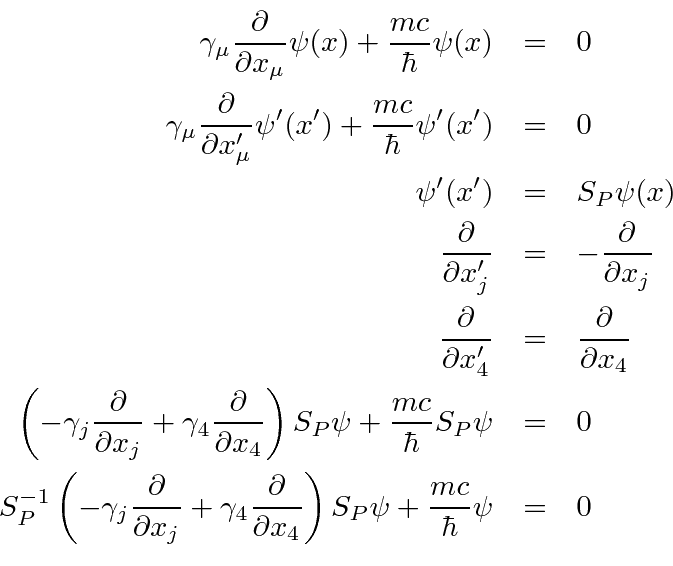
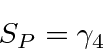
Therefore, under a parity inversion operation
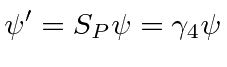 |
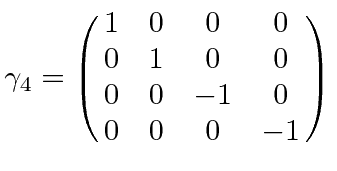 ,
the third and fourth components of the spinor change sign while the first two don't.
Since we could have chosen
,
the third and fourth components of the spinor change sign while the first two don't.
Since we could have chosen
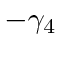 , all we know is that
components 3 and 4 have the opposite parity of components 1 and 2.
, all we know is that
components 3 and 4 have the opposite parity of components 1 and 2.
Jim Branson 2013-04-22