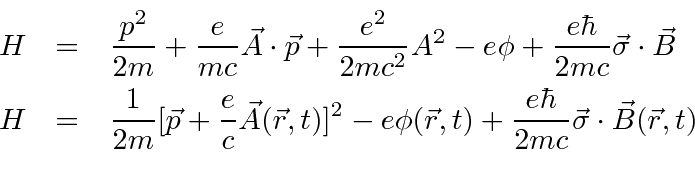In the homework on electrons in an electromagnetic field, we showed that
the Schrödinger-Pauli Hamiltonian gives the same result as the non-relativistic Hamiltonian we have been using
and automatically includes the interaction of the electron's spin with the magnetic field.
The derivation is repeated here.
Recall that
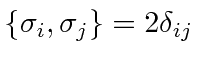 ,
,
![\bgroup\color{black}$[\sigma_i,\sigma_j]=2\epsilon_{ijk}\sigma_k$\egroup](img4167.png) , and that the momentum operator
differentiates both
, and that the momentum operator
differentiates both
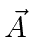 and the wavefunction.
and the wavefunction.
We assume the Lorentz condition applies.
This is a step in the right direction.
The wavefunction now has two components (a spinor) and the effect of spin is included.
Note that this form of the NR Hamiltonian yields the coupling of the electron spin to a magnetic field
with the correct 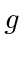 factor of 2.
The spin-orbit interaction can be correctly derived from this.
factor of 2.
The spin-orbit interaction can be correctly derived from this.
Jim Branson
2013-04-22
![\bgroup\color{black}$\displaystyle H={1\over 2m}\left(\vec{\sigma}\cdot[\vec{p}+{e\over c}\vec{A}(\vec{r},t)]\right)^2-e\phi(\vec{r},t)$\egroup](img4165.png)
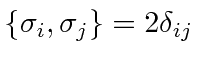 ,
,
![\bgroup\color{black}$[\sigma_i,\sigma_j]=2\epsilon_{ijk}\sigma_k$\egroup](img4167.png) , and that the momentum operator
differentiates both
, and that the momentum operator
differentiates both
![\begin{eqnarray*}
\left(\vec{\sigma}\cdot[\vec{p}+{e\over c}\vec{A}(\vec{r},t)]\...
...}\vec{A}\cdot\vec{p}+{e\hbar\over c}\vec{\sigma}\cdot\vec{B} \\
\end{eqnarray*}](img4168.png)