Dirac's Motivation

The Schrödinger equation is simply the non-relativistic energy equation operating on a wavefunction.

$$\bgroup\color{black} E={p^2\over 2m}+V(\vec{r}) \egroup$$

The natural extension of this is the relativistic energy equation.

$$\bgroup\color{black} E^2=p^2c^2+(mc^2)^2 \egroup$$

This is just the Klein-Gordon equation that we derived for a scalar field. It did not take physicists long to come up with this equation.

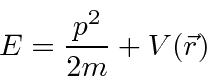
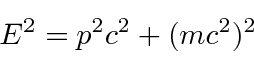
Because the Schrödinger equation is first order in the time derivative, the initial conditions needed to determine a solution to the equation are just 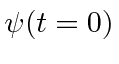$\psi(t=0)$. In an equation that is second order in the time derivative, we also need to specify some information about the time derivatives at $t=0$ to determine the solution at a later time. It seemed strange to give up the concept that all information is contained in the wave function to go to the relativistically correct equation.

If we have a complex scalar field that satisfies the (Euler-Lagrange = Klein-Gordon) equations

$$\begin{eqnarray*} \Box\phi-m^2\phi&=&0 \\ \Box\phi^*-m^2\phi^*&=&0, \\ \end{eqnarray*}$$

it can be shown that the bilinear quantity

$$\bgroup\color{black} s_\mu={\hbar\over 2mi}\left(\phi^*{\part... ...l x_\mu}-{\partial\phi^*\over\partial x_\mu}\phi\right) \egroup$$

satisfies the flux conservation equation

$$\bgroup\color{black} {\partial s_\mu\over\partial x_\mu}={\hb... ...{\hbar\over 2mi}m^2\left(\phi^*\phi-\phi^*\phi\right)=0 \egroup$$

and reduces to the probability flux we used with the Schrödinger equation, in the non-relativistic limit. The fourth component of the vector is just $c$ times the probability density, so that's fine too (using $e^{imc^2t/\hbar}$ as the time dependence.).

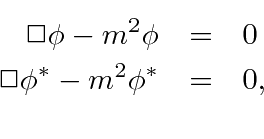
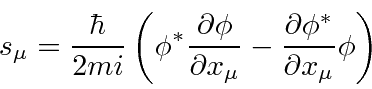
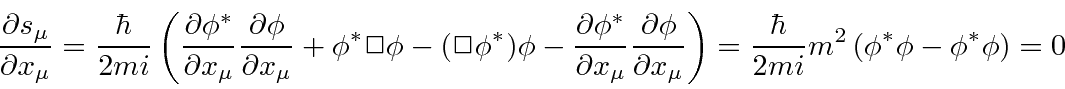
The perceived problem with this probability is that it is not always positive. Because the energy operator appears squared in the equation, both positive energies and negative energies are solutions. Both solutions are needed to form a complete set. With negative energies, the probability density is negative. Dirac thought this was a problem. Later, the vector $s_\mu$ was reinterpreted as the electric current and charge density, rather than probability. The Klein-Gordon equation was indicating that particles of both positive and negative charge are present in the complex scalar field. The ``negative energy solutions'' are needed to form a complete set, so they cannot be discarded.

Dirac sought to solve the perceived problem by finding an equation that was somehow linear in the time derivative as is the Schrödinger equation. He managed to do this but still found ``negative energy solutions'' which he eventually interpreted to predict antimatter. We may also be motivated to naturally describe particles with spin one-half.