Next: Raman Effect Up: Scattering of Photons Previous: Rayleigh Scattering Contents
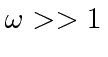 eV.
then cross section approaches that for scattering from a free electron, Thomson Scattering.
We still neglect the effect of electron recoil so we should also require that
eV.
then cross section approaches that for scattering from a free electron, Thomson Scattering.
We still neglect the effect of electron recoil so we should also require that
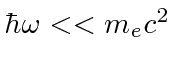 .
Start from the Kramers-Heisenberg formula.
.
Start from the Kramers-Heisenberg formula.
![\begin{displaymath}\bgroup\color{black} {d\sigma\over d\Omega}
= \left({e^2\over...
...angle
\over \omega_{ji}+\omega'}
\right] \right\vert^2 \egroup\end{displaymath}](img464.png)
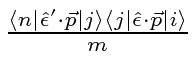 which is of the order of the electron's kinetic energy,
so we can ignore the second two terms.
(Even if the intermediate and final states have unbound electrons, the initial state wave function will keep these terms small.)
which is of the order of the electron's kinetic energy,
so we can ignore the second two terms.
(Even if the intermediate and final states have unbound electrons, the initial state wave function will keep these terms small.)
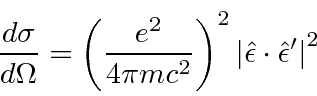
The only dependence is on polarization.
This is a good time to take a look at the meaning of the polarization vectors we've been carrying around in the calculation
and at the lack of any wave-vectors for the initial and final state.
A look back at the calculation shows that we calculated the transition rate from a state with one photon with
wave-vector
![]() and polarization
and polarization
![]() to a final state with polarization
to a final state with polarization
![]() .
We have integrated over the final state wave vector magnitude, subject to the delta function giving energy conservation,
but, we have not integrated over final state photon direction yet, as indicated by the
.
We have integrated over the final state wave vector magnitude, subject to the delta function giving energy conservation,
but, we have not integrated over final state photon direction yet, as indicated by the
![]() .
There is no explicit angular dependence but there is some
hidden in the dot product between initial and final polarization vectors, both of which must be transverse
to the direction of propagation.
We are ready to compute four different differential cross sections
corresponding to two initial polarizations times two final state photon polarizations.
Alternatively, we average and/or sum, if we so choose.
.
There is no explicit angular dependence but there is some
hidden in the dot product between initial and final polarization vectors, both of which must be transverse
to the direction of propagation.
We are ready to compute four different differential cross sections
corresponding to two initial polarizations times two final state photon polarizations.
Alternatively, we average and/or sum, if we so choose.
In the high energy approximation we have made, there is no dependence on the state of the atoms,
so we are free to choose our coordinate system any way we want.
Set the z-axis to be along the direction of the initial photon
and set the x-axis so that the scattered photon is in the x-z plane (
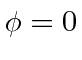 ).
The scattered photon is at an angle
).
The scattered photon is at an angle
![]() to the initial photon direction and at
to the initial photon direction and at
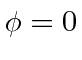 .
A reasonable set of initial state polarization vectors is
.
A reasonable set of initial state polarization vectors is
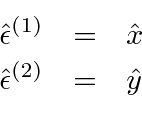
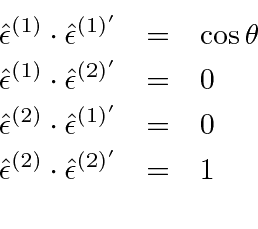
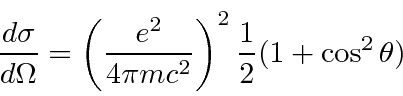
Even if the initial state is unpolarized, the final state can be polarized.
For example, for
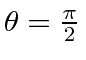 , all of the above dot products are zero except
, all of the above dot products are zero except
![]() .
That means only the initial photons polarized along the y direction will scatter and that
the scattered photon is 100% polarized transverse to the scattering plane(really just the same polarization as the initial state).
The angular distribution could also be used to deduce the polarization of the initial state if a large ensemble of
initial state photons were available.
.
That means only the initial photons polarized along the y direction will scatter and that
the scattered photon is 100% polarized transverse to the scattering plane(really just the same polarization as the initial state).
The angular distribution could also be used to deduce the polarization of the initial state if a large ensemble of
initial state photons were available.
For a definite initial state polarization (at an angle
![]() to the scattering plane, the component along
to the scattering plane, the component along
![]() is
is
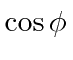 and along
and along
![]() is
is
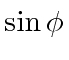 .
If we don't observe final state polarization we sum
.
If we don't observe final state polarization we sum
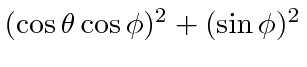 and have
and have
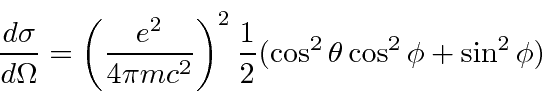
For atoms with more than one electron, this cross section will grow as
![]() .
.
Jim Branson 2013-04-22