Next: Quantum Theory of Radiation Up: Classical Maxwell Fields Previous: The Lagrangian for Electromagnetic Contents
We have already studied many aspects of
gauge invariance
in electromagnetism and the corresponding
invariance under a phase transformation in Quantum Mechanics.
One point to note is that, with our choice to ``treat each component of
![]() as an independent field'',
we are making a theory for the vector field
as an independent field'',
we are making a theory for the vector field ![]() with a gauge symmetry,
not really a theory for the field
with a gauge symmetry,
not really a theory for the field
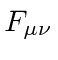 .
.
Recall that the gauge symmetry of Electricity and Magnetism and the phase symmetry of electron wavefunctions are really one and the same. Neither the phase of the wavefunction nor the vector potential are directly observable, but the symmetry is.
We will not go over the consequences of gauge invariance again here, but, we do want to use gauge invariance to simplify our equations.
Maxwell's equation is
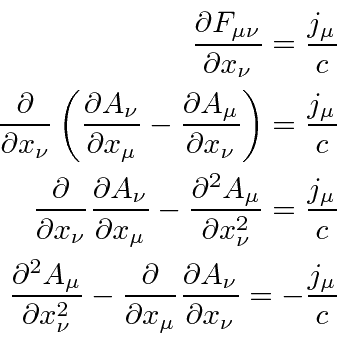
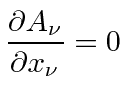 |
![\begin{eqnarray*}
A_\mu\rightarrow A_\mu+{\partial\chi\over\partial x_\mu} \\
\Box\chi=-\left[{\partial A_\nu\over\partial x_\nu}\right]_{old} \\
\end{eqnarray*}](img3866.png)
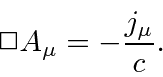
There is still substantial gauge freedom possible.
The second derivative of
![]() is set by the Lorentz condition but there is still freedom
in the first derivative which will modify
is set by the Lorentz condition but there is still freedom
in the first derivative which will modify
![]() .
Gauge transformations can be made as shown below.
.
Gauge transformations can be made as shown below.
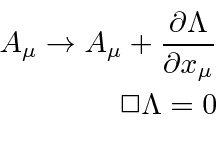
Jim Branson 2013-04-22