Next: The Electromagnetic Field Tensor Up: Classical Maxwell Fields Previous: Classical Maxwell Fields Contents
The SI units are based on a unit of length of the order of human size originally related to the size of the earth,
a unit of time approximately equal to the time between heartbeats,
and a unit of mass related to the length unit and the mass of water.
None of these depend on any even nearly fundamental physical quantities.
Therefore many important physical equations end up with extra (needless) constants in them like
![]() .
Even with the three basic units defined, we could have chosen the unit of charge correctly to make
.
Even with the three basic units defined, we could have chosen the unit of charge correctly to make
![]() and
and
![]() unnecessary but instead a very arbitrary choice was made
unnecessary but instead a very arbitrary choice was made
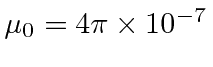 and the Ampere is defined by the current in parallel wires at one meter distance from each other that gives a force of
and the Ampere is defined by the current in parallel wires at one meter distance from each other that gives a force of
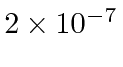 Newtons per meter. The Coulomb is set so that the Ampere is one Coulomb per second.
With these choices SI units make Maxwell's equations and our filed theory look very messy.
Newtons per meter. The Coulomb is set so that the Ampere is one Coulomb per second.
With these choices SI units make Maxwell's equations and our filed theory look very messy.
Physicists have more often used CGS units in which the unit of charge and definition of the field units are set
so that
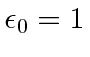 and
and
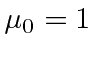 so they need not show up in the equations.
The CGS units are not perfect, however, and we will want to change them slightly to make our theory of the Maxwell Field simple.
The mistake made in defining CGS units was in removing the
so they need not show up in the equations.
The CGS units are not perfect, however, and we will want to change them slightly to make our theory of the Maxwell Field simple.
The mistake made in defining CGS units was in removing the
![]() that show up in Coulombs law.
Coulombs law is not fundamental and the
that show up in Coulombs law.
Coulombs law is not fundamental and the
![]() belonged there.
belonged there.
We will correct this little mistake and move to Rationalized Heaviside-Lorentz Units by
making a minor modification to the unit of charge and the units of fields.
With this modification, our field theory will have few constants to carry around.
As the name of the system of units suggests, the problem with CGS has been with
![]() .
We don't need to change the centimeter, gram or second to fix the problem.
.
We don't need to change the centimeter, gram or second to fix the problem.
In Rationalized Heaviside-Lorentz units we decrease the field strength by a factor of
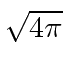 and increase the charges by the same factor, leaving the force unchanged.
and increase the charges by the same factor, leaving the force unchanged.
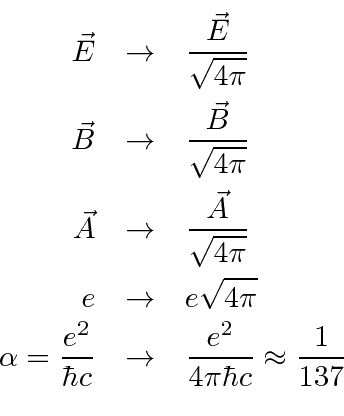
Maxwell's Equations in CGS units are
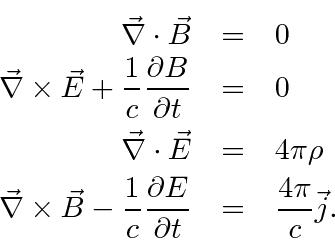
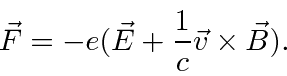
When we change to Rationalized Heaviside-Lorentz units, the equations become
|
|
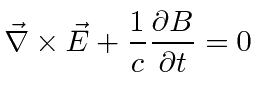
|
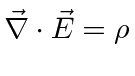
|
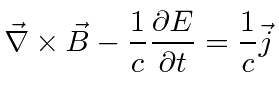
|
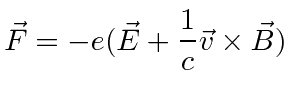 |
Jim Branson 2013-04-22