LASERs

Light Amplification through Stimulated Emission of Radiation is the phenomenon with the acronym LASER. As the name would indicate, the LASER uses stimulated emission to genrate an intense pulse of light. Our equations show that the decay rate of a state by emission of a photon is proportional to the number (plus one) of photons in the field (with the same wave-number as the photon to be emitted).

$$\begin{eqnarray*} \vec{A}(\vec{r},t)&=&\left[{2\pi\hbar c^2\over\omega V}\right]... ...\omega t)}+\sqrt{N+1}e^{-i(\vec{k}\cdot\vec{r}-\omega t)}\right) \end{eqnarray*}$$

Here ``plus one'' is not really important since the number of photons is very large.

Lets assume the material we wish to use is in a cavity. Assume this material has an excited state that can decay by the emission of a photon to the ground state. In normal equilibrium, there will be many more atoms in the ground state and transitions from one state to the other will be in equilibrium and black body radiation will exist in the cavity. We need to circumvent equilibrium to make the LASER work. To cause many more photons to be emitted than are reabsorbed a LASER is designed to produce a poplation inversion. That is, we find a way to put many more atoms in the excited state than would be the case in equilibrium.

If this population inversion is achieved, the emission from one atom will increase the emission rate from the other atoms and that emission will stimulate more. In a pulsed laser, the population of the excited state will become depleted and the light pulse will end until the inversion can be achieved again. If the population of the excited state can be continuously pumped up, then the LASER can run continously.

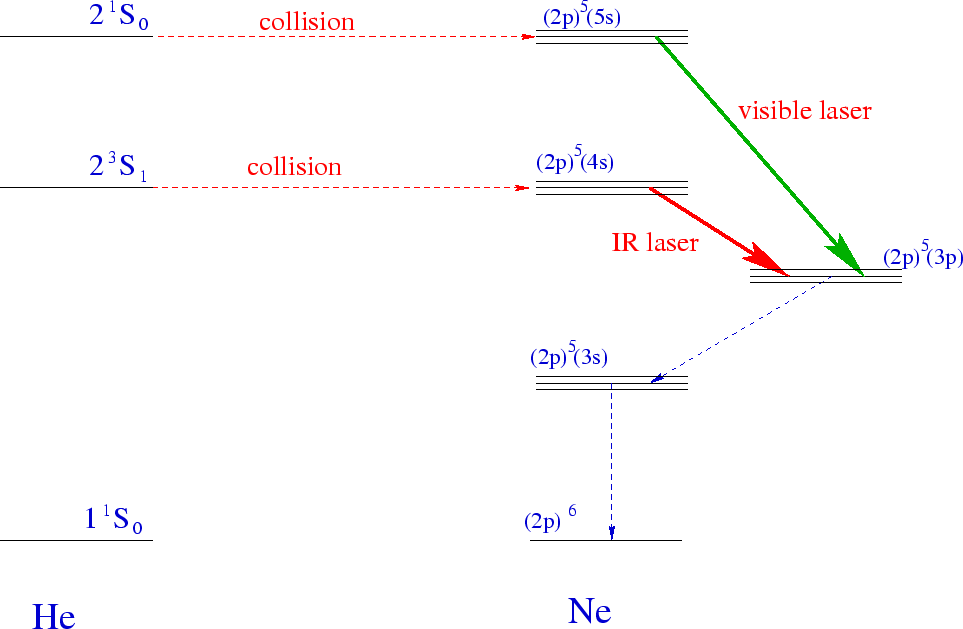
This optical pumping to achieve a population inversion can be done in a number of ways. For example, a Helium-Neon LASER has a mixture of the two gasses. If a high voltage is applied and an electric current flows through the gasses, both atoms can be excited. It turns out that the first and second excited states of Helium have almost the same excitation energy as the 4s and 5s excitations of Neon. The Helium states can't make an E1 transition so they are likely to excite a Neon atom instead. An excited Helium atom can de-excite in a collision with a Neon atom, putting the Neon in a highly excited state. Now there is a population inversion in the Neon. The Neon decays more quickly so its de-excitation is dominated by photon emission.

Another way to get the population inversion is just the use of a metastable state as in a ruby laser. A normal light sorce can excite a higher excited state which decays to a metastable excited state. The metastable state will have a much larger population than in equilibrium.

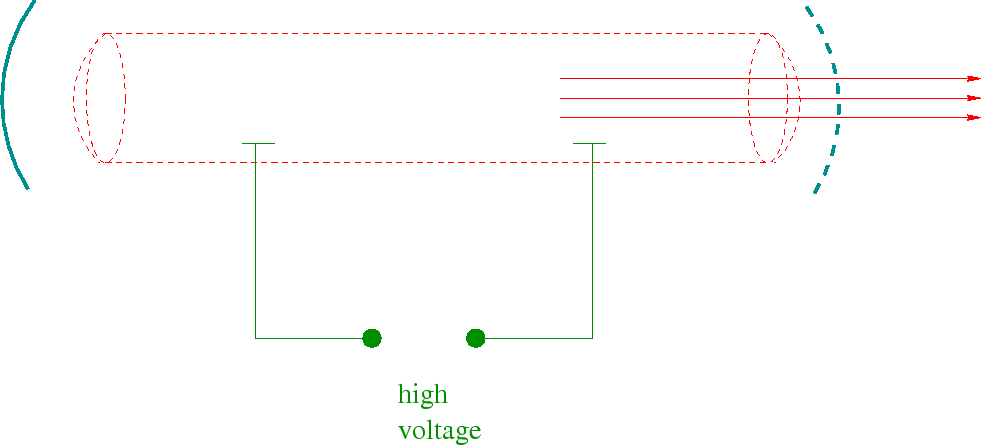
A laser with a beam coming out if it would be made in a cavity with a half silvered mirror so that the radiation can build up inside the cavity, but some of the radiation leaks out to make the beam.