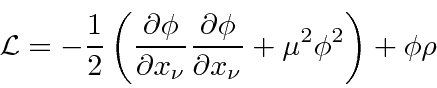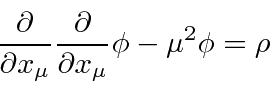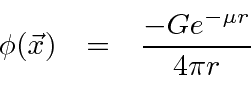A
review of classical field theory
is useful to ground our development of relativistic quantum field theories for photons and electrons.
We will work with 4-vectors like the coordinate vector below
using the
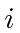 to get a
to get a
 in the time term in a dot product (instead of using a metric tensor).
in the time term in a dot product (instead of using a metric tensor).
A Lorentz scalar Lagrangian density will be derived for each field theory we construct.
From the Lagrangian we can derive a field equation called the Euler-Lagrange equation.
The Lagrangian for a massive scalar field
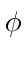 can be deduced from the requirement that it be a scalar
can be deduced from the requirement that it be a scalar
where the last term is the interaction with a source.
The Euler-Lagrange equation gives
which is the known as the Klein-Gordon equation with a source
and is a reasonable relativistic equation for a scalar field.
Using Fourier transforms, the field from a point source can be computed.
This is a field that falls off much faster than
 .
A massive scalar field falls off exponentially and the larger the mass, the faster the fall off.
This fits the form of the force between nucleons fairly well although the actual nuclear force needs a much more
detailed study.
.
A massive scalar field falls off exponentially and the larger the mass, the faster the fall off.
This fits the form of the force between nucleons fairly well although the actual nuclear force needs a much more
detailed study.
Jim Branson
2013-04-22
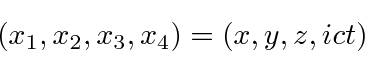
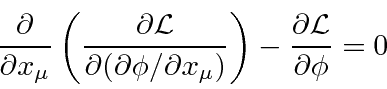
![]() can be deduced from the requirement that it be a scalar
can be deduced from the requirement that it be a scalar