- Two identical spin
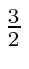 particles are bound together
into a state with total angular momentum
particles are bound together
into a state with total angular momentum 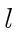 .
a) What are the allowed states of total spin for
.
a) What are the allowed states of total spin for 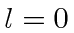 and for
and for 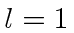 ?
b) List the allowed states using spectroscopic notation for
?
b) List the allowed states using spectroscopic notation for 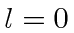 and 1.
and 1.
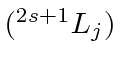
- A hydrogen atom is in the state
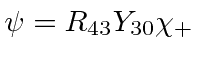 .
A combined measurement of of
.
A combined measurement of of 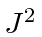 and of
and of 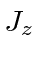 is made.
What are the possible outcomes of this combined measurement
and what are the probabilities of each?
You may ignore nuclear spin in this problem.
is made.
What are the possible outcomes of this combined measurement
and what are the probabilities of each?
You may ignore nuclear spin in this problem.
- We want to find the eigenstates of total
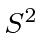 and
and 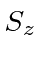 for two spin 1 particles
which have an
for two spin 1 particles
which have an 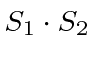 interaction. (
interaction. (
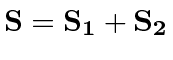 )
)
- What are the allowed values of
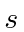 , the total spin quantum number.
, the total spin quantum number.
- Write down the states of maximum
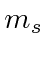 for the maximum
for the maximum 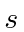 state.
Use
state.
Use 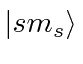 notation and
notation and
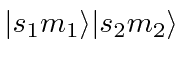 for
the product states.
for
the product states.
- Now apply the lowering operator to get the other
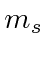 states. You
only need to go down to
states. You
only need to go down to 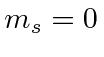 because of the obvious symmetry.
because of the obvious symmetry.
- Now find the states with the other values of
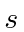 in a similar way.
in a similar way.
- Two (identical) electrons are bound in a Helium atom.
What are the allowed states
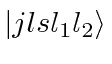 if both electrons have
principal quantum number
if both electrons have
principal quantum number 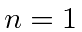 ?
What are the states if one has
?
What are the states if one has 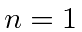 and the other
and the other 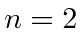 ?
?
- A hydrogen atom is in an eigenstate
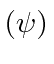 of
of 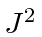 ,
, 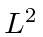 , and of
, and of 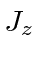 such that
such that
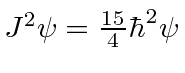 ,
,
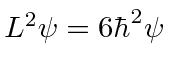 ,
,
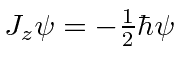 ,
and of course the electron's spin is
,
and of course the electron's spin is 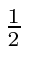 .
Determine the quantum numbers of this state as well as you can.
If a measurement of
.
Determine the quantum numbers of this state as well as you can.
If a measurement of 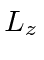 is made, what are the possible outcomes and
what are the probabilities of each.
is made, what are the possible outcomes and
what are the probabilities of each.
- A hydrogen atom is in the state
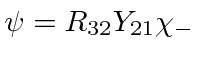 .
If a measurement of
.
If a measurement of 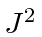 and of
and of 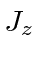 is made, what are the possible outcomes
of this measurement and what are the probabilities for each outcome?
If a measurement of the energy of the state is made, what are the possible
energies and the probabilities of each? You may ignore the nuclear spin
in this problem.
is made, what are the possible outcomes
of this measurement and what are the probabilities for each outcome?
If a measurement of the energy of the state is made, what are the possible
energies and the probabilities of each? You may ignore the nuclear spin
in this problem.
- Two identical spin 1 particles are bound together into a
state with orbital angular momentum
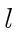 . What are the allowed states
of total spin (s) for
. What are the allowed states
of total spin (s) for 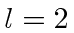 , for
, for 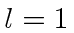 , and for
, and for 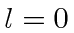 ? List all the
allowed states giving, for each state, the values of the quantum numbers for
total angular momentum
? List all the
allowed states giving, for each state, the values of the quantum numbers for
total angular momentum 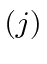 , orbital angular momentum
, orbital angular momentum 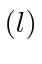 and
spin angular momentum
and
spin angular momentum 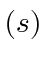 if
if 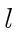 is 2 or less. You need not list all the
different
is 2 or less. You need not list all the
different 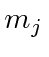 values.
values.
- List all the allowed states of total spin and
total z-component of spin for 2 identical spin 1 particles.
What
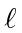 values are allowed for each of these states?
Explicitly write down the
values are allowed for each of these states?
Explicitly write down the 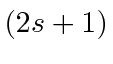 states
for the highest
states
for the highest 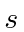 in terms of
in terms of
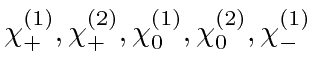 , and
, and
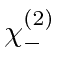 .
.
- Two different spin
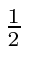 particles have a Hamiltonian
given by
particles have a Hamiltonian
given by
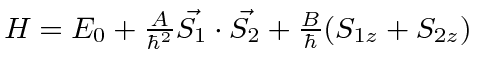 .
Find the allowed energies and the energy eigenstates in terms of the four
basis states
.
Find the allowed energies and the energy eigenstates in terms of the four
basis states 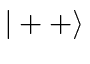 ,
, 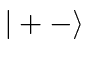 ,
, 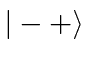 , and
, and 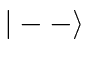 .
.
- A spin 1 particle is in an
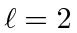 state.
Find the allowed values of the total angular momentum quantum number,
state.
Find the allowed values of the total angular momentum quantum number, 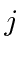 .
Write out the
.
Write out the 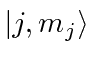 states for the largest allowed
states for the largest allowed 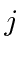 value,
in terms of the
value,
in terms of the
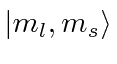 basis.
(That is give one state for every
basis.
(That is give one state for every 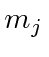 value.)
If the particle is prepared in the state
value.)
If the particle is prepared in the state
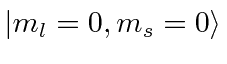 ,
what is the probability to measure
,
what is the probability to measure 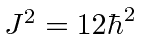 ?
?
- Two different spin
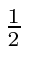 particles have a Hamiltonian
given by
particles have a Hamiltonian
given by
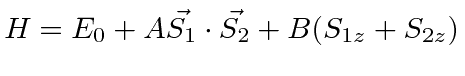 .
Find the allowed energies and the energy eigenstates in terms of the four
product states
.
Find the allowed energies and the energy eigenstates in terms of the four
product states
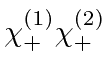 ,
,
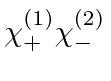 ,
,
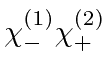 , and
, and
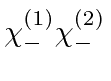 .
.
Jim Branson
2013-04-22
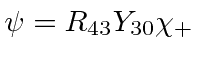 .
A combined measurement of of
.
A combined measurement of of 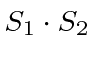 interaction. (
interaction. (
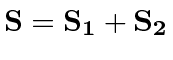 )
)
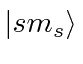 notation and
notation and
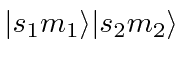 for
the product states.
for
the product states.
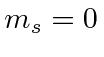 because of the obvious symmetry.
because of the obvious symmetry.
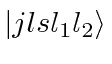 if both electrons have
principal quantum number
if both electrons have
principal quantum number  of
of 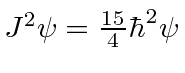 ,
,
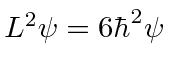 ,
,
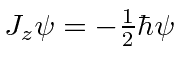 ,
and of course the electron's spin is
,
and of course the electron's spin is 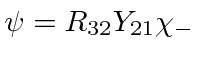 .
If a measurement of
.
If a measurement of 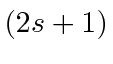 states
for the highest
states
for the highest 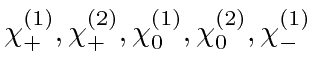 , and
, and
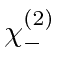 .
.
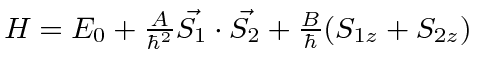 .
Find the allowed energies and the energy eigenstates in terms of the four
basis states
.
Find the allowed energies and the energy eigenstates in terms of the four
basis states 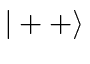 ,
, 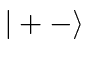 ,
, 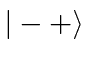 , and
, and 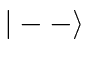 .
.
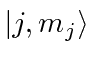 states for the largest allowed
states for the largest allowed 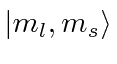 basis.
(That is give one state for every
basis.
(That is give one state for every 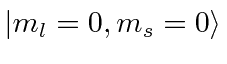 ,
what is the probability to measure
,
what is the probability to measure 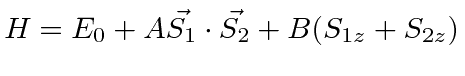 .
Find the allowed energies and the energy eigenstates in terms of the four
product states
.
Find the allowed energies and the energy eigenstates in terms of the four
product states
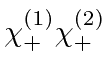 ,
,
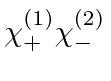 ,
,
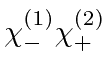 , and
, and
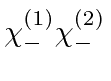 .
.