Time Independent Perturbation Theory

Assume we have already solved and an energy eigenvalue problem and now need to include an additional term in the Hamiltonian. We can use time independent perturbation theory to calculate corrections to the energy eigenvalues and eigenstates. If the Schrödinger equation for the full problem is

$$\bgroup\color{black}(H_0+H_1)\psi_n=E_n\psi_n\egroup$$

and we have already solved the eigenvalue problem for $H_0$, we may use a perturbation series,to expand both our energy eigenvalues and eigenstates in powers of the small perturbation.

$$\begin{eqnarray*} & E_n=E_n^{(0)}+E_n^{(1)}+E_n^{(2)}+... \\ & \psi_n=N\left(\p... ...n}c_{nk}\phi_k\right) \\ & c_{nk}=c_{nk}^{(1)}+c_{nk}^{(2)}+... \end{eqnarray*}$$

where the superscript (0), (1), (2) are the zeroth, first, and second order terms in the series. $N$ is there to keep the wave function normalized but will not play an important role in our results.

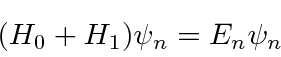
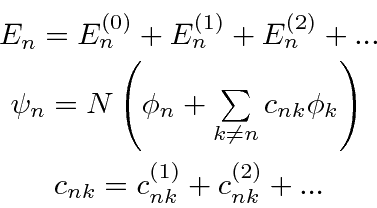
By solving the Schrödinger equation at each order of the perturbation series, we compute the corrections to the energies and eigenfunctions. We just give the first few terms above.

$$\begin{eqnarray*} & E_n^{(1)}=\langle\phi_n\vert H_1\vert\phi_n\rangle \\ & c_{... ..._k\vert H_1\vert\phi_n\rangle\vert^2 \over E_n^{(0)}-E_k^{(0)}} \end{eqnarray*}$$

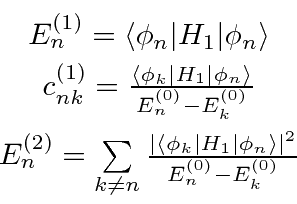
A problem arises in the case of degenerate states or nearly degenerate states. The energy denominator in the last equation above is small and the series does not converge. To handle this case, we need to rediagonalize the full Hamiltonian in the subspace of nearly degenerate states.

$$\bgroup\color{black}\sum\limits_{i\in{\cal N}}\langle\phi_n^{(j)}\vert H\vert\phi_n^{(i)}\rangle\alpha_i=E_n\alpha_j.\egroup$$

This is just the standard eigenvalue problem for the full Hamiltonian in the subspace of (nearly) degenerate states.

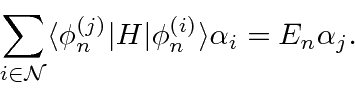
We will use time independent perturbation theory is used to compute fine structure and hyperfine corrections to Hydrogen energies, as well as for many other calculations. Degenerate state perturbation theory will be used for the Stark Effect and for hyperfine splitting in Hydrogen.