Adding the Spins of Two Electrons

$\begin{displaymath}\bgroup\color{black}[S_{(1)i},S_{(2)j}]=0\egroup\end{displaymath}$

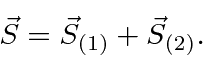
$\begin{displaymath}\bgroup\color{black}\vec{S}=\vec{S}_{(1)}+\vec{S}_{(2)}.\egroup\end{displaymath}$

$\begin{displaymath}\bgroup\color{black}[S_{i},S_{j}]=i\hbar\epsilon_{ijk}S_k.\egroup\end{displaymath}$

This is a very important result since we derived everything about angular momentum from the commutators. The sum of angular momentum will be quantized in the same way as orbital angular momentum.

As with the combination of independent spatial coordinates, we can make product statesto describe the spins of two particles. These products just mean, for example, the spin of particle 1 is up and the spin of particle 2 is down. There are four possible (product) spin states when we combine two spin $\bgroup\color{black}${1\over 2}$\egroup$ particles. These product states are eigenstates of total but not necessarily of total $\bgroup\color{black}$S^2$\egroup$ . The states and their $\bgroup\color{black}$S_z$\egroup$ eigenvalues are given below.

Product State	Total $\bgroup\color{black}$S_z$\egroup$ eigenvalue
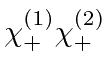$\bgroup\color{black}$\chi^{(1)}_+\chi^{(2)}_+$\egroup$	$\bgroup\color{black}$\hbar$\egroup$
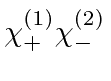$\bgroup\color{black}$\chi^{(1)}_+\chi^{(2)}_-$\egroup$	$\bgroup\color{black}$0$\egroup$
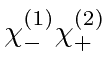$\bgroup\color{black}$\chi^{(1)}_-\chi^{(2)}_+$\egroup$	$\bgroup\color{black}$0$\egroup$
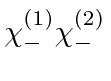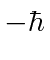$\bgroup\color{black}$\chi^{(1)}_-\chi^{(2)}_-$\egroup$	$\bgroup\color{black}$-\hbar$\egroup$

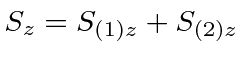Verify the quoted eigenvalues by calculation using the operator $S_z=S_{(1)z}+S_{(2)z}$ .

We expect to be able to form eigenstates of from linear combinations of these four states. From pure counting of the number of states for each $\bgroup\color{black}$S_z$\egroup$ eigenvalue, we can guess that we can make one $\bgroup\color{black}$s=1$\egroup$ multiplet plus one $\bgroup\color{black}$s=0$\egroup$ multiplet. The $\bgroup\color{black}$s=1$\egroup$ multiplet has three component states, two of which are obvious from the list above. We can use the lowering operator to derive the other eigenstates of

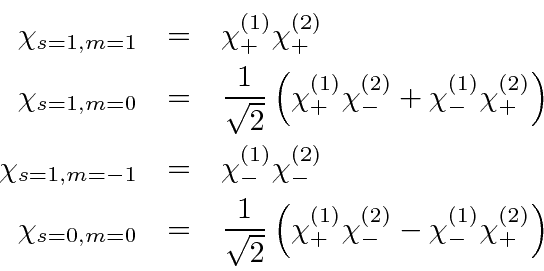
$\begin{eqnarray*} \chi_{s=1,m=1}&=&\chi^{(1)}_+\chi^{(2)}_+ \\ \chi_{s=1,m=0}&=... ...}}\left(\chi^{(1)}_+\chi^{(2)}_-\chi^{(1)}_-\chi^{(2)}_+\right) \end{eqnarray*}$

As a necessary check, we operate on these states with $\bgroup\color{black}$S^2$\egroup$ and verify that they are indeed the correct eigenstates.

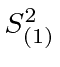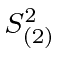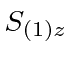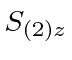Note that by deciding to add the spins together, we could not change the nature of the electrons. They are still spin $\bgroup\color{black}${1\over 2}$\egroup$ and hence, these are all still eigenstates of $\bgroup\color{black}$S_{(1)}^2$\egroup$ and $\bgroup\color{black}$S_{(2)}^2$\egroup$ , however, (some of) the above states are not eigenstates of $\bgroup\color{black}$S_{(1)z}$\egroup$ and $\bgroup\color{black}$S_{(2)z}$\egroup$ . This will prove to be a general feature of adding angular momenta. Our states of definite total angular momentum and z component of total angular momentum will still also be eigenstates of the individual angular momenta squared.