Next: Applying the Operator to Up: Derivations and Computations Previous: Commutators of Total Spin Contents
The total spin lowering operator is
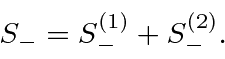
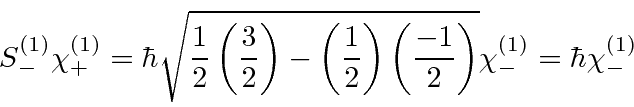
Now we want to identify
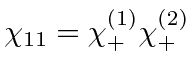 .
Lets operate on this equation with
.
Lets operate on this equation with
![]() . First the RHS gives
. First the RHS gives
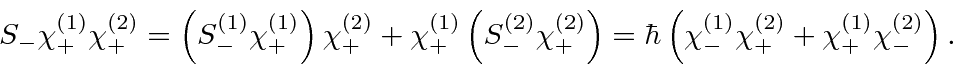
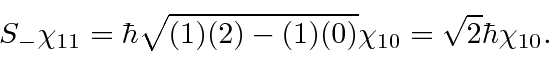
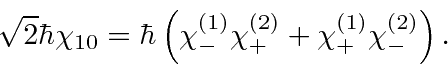
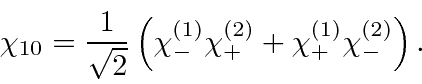
Now we can lower this state.
Lowering the LHS, we get
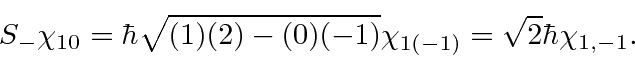
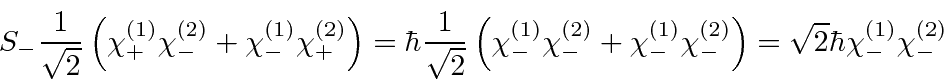
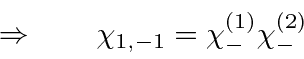
There is one state left over which is orthogonal to the three states we identified.
Orthogonal state:
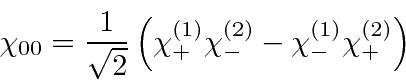
Jim Branson 2013-04-22