Partial Wave Analysis of Scattering *

We can take a quick look at scattering from a potential in 3DWe assume that $V=0$ far from the origin so the incoming and outgoing waves can be written in terms of our solutions for a constant potential.

In fact, an incoming plane wave along the $z$ direction can be expanded in Bessel functions.

$$e^{ikz}=e^{ikr\cos\theta}=\sum\limits_{\ell=0}^\infty\sqrt{4\pi(2\ell+1)}i^\ell j_\ell(kr)Y_{\ell 0}$$

Each angular momentum $(\ell)$ term is called a partial wave. The scattering for each partial wave can be computed independently.

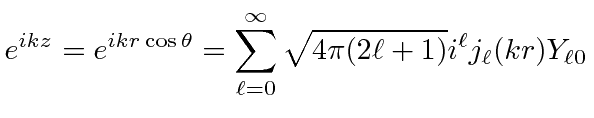For large $r$ the Bessel function becomes

$$\bgroup\color{black} j_\ell(\rho)\rightarrow -{1\over 2ikr}\left(e^{-i(kr-\ell\pi/2)}-e^{i(kr-\ell\pi/2)}\right) ,\egroup$$

so our plane wave becomes

$$\bgroup\color{black}e^{ikz}\rightarrow -\sum\limits_{\ell=0}^... ...{-i(kr-\ell\pi/2)}-e^{i(kr-\ell\pi/2)}\right)Y_{\ell 0} \egroup$$

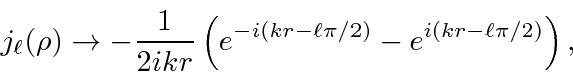
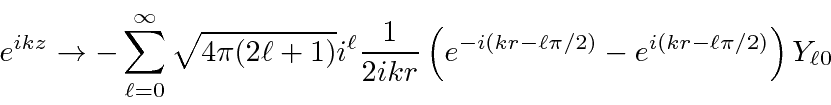
The scattering potential will modify the plane wave, particularly the outgoing part. To maintain the outgoing flux equal to the incoming flux, the most the scattering can do is change the relative phase of the incoming an outgoing waves.

$$\bgroup\color{black}R_\ell(r)\rightarrow-{1\over 2ikr}\left(e... ...l\pi/2)}-e^{2i\delta_\ell(k)}e^{i(kr-\ell\pi/2)}\right) \egroup$$

$$\bgroup\color{black}={\sin(kr-\ell\pi/2+\delta_\ell(k))\over kr}e^{i\delta_\ell(k)} \egroup$$

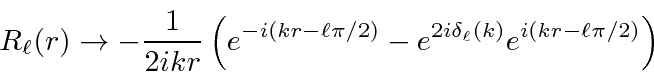
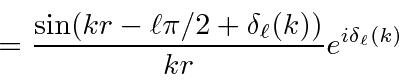
The 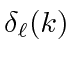$\delta_\ell(k)$ is called the phase shift for the partial wave of angular momentum $\ell$. We can compute the differential cross section for scattering

$$\bgroup\color{black}{d\sigma\over d\Omega}\equiv{{\rm scattered flux into }d\Omega\over{\rm incident flux}} \egroup$$

in terms of the phase shifts.

$${d\sigma\over d\Omega}={1\over k^2}\left\brac... ...1)e^{i\delta_\ell}\sin(\delta_\ell)P_\ell(\cos\theta)\right\bracevert^2$$

The phase shifts must be computed by actually solving the problem for the particular potential.

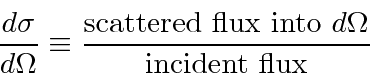
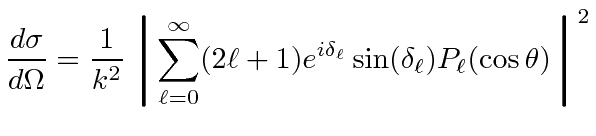In fact, for low energy scattering and short range potentials, the first term $\ell=0$ is often enough to solve the problem.

Only the low $\ell$ partial waves get close enough to the origin to be affected by the potential.