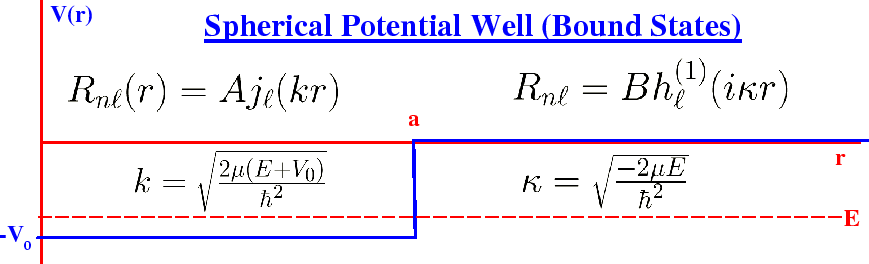
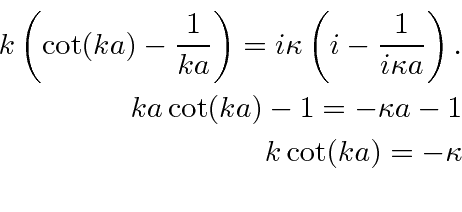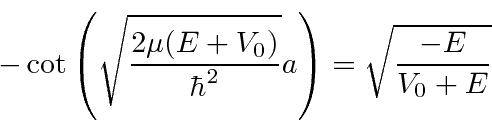We now wish to find the energy eigenstates for
a spherical potential well of radius
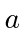 and potential
and potential
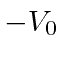 .
We must use the Bessel function near the origin.
.
We must use the Bessel function near the origin.
We must use the Hankel function of the first type for large
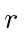 .
.
To solve the problem, we have to match the solutions at the boundary.
First match the wavefunction.
Then match the first derivative.
We can divide the two equations to eliminate the constants to get a condition on the energies.
This is often called matching the logarithmic derivative.
Often, the
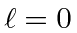 term will be sufficient to describe scattering.
For
term will be sufficient to describe scattering.
For
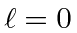 , the boundary condition is
, the boundary condition is
Dividing and substituting for
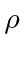 , we get
, we get
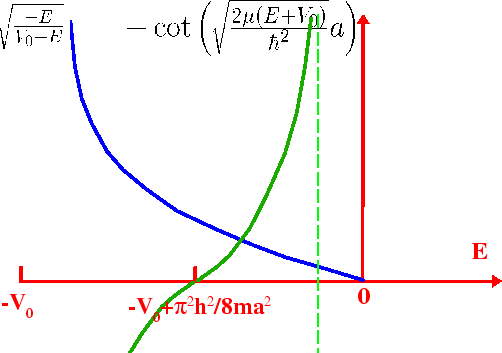
This is the same transcendental equation that we had for the odd solution in one dimension.
The number of solutions depends on the depth and radius of the well.
There can even be no solution.
Jim Branson
2013-04-22
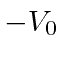 .
.
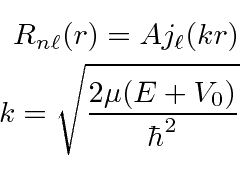
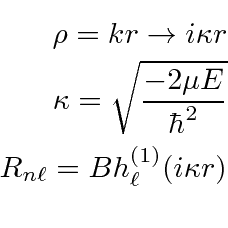
![\begin{displaymath}\bgroup\color{black}A\left[j_\ell(\rho)\right]_{\rho=ka}=B\left[h_\ell(\rho)\right]_{\rho=i\kappa a} \egroup\end{displaymath}](img1893.png)
![\begin{displaymath}\bgroup\color{black}Ak\left[{dj_\ell(\rho)\over d\rho}\right]...
...left[{dh_\ell(\rho)\over d\rho}\right]_{\rho=i\kappa a} \egroup\end{displaymath}](img1894.png)
![\begin{displaymath}\bgroup\color{black}k\left[{{dj_\ell(\rho)\over d\rho}\over j...
...\over d\rho}\over h_\ell(\rho)}\right]_{\rho=i\kappa a} \egroup\end{displaymath}](img1895.png)
![]() term will be sufficient to describe scattering.
For
term will be sufficient to describe scattering.
For
![]() , the boundary condition is
, the boundary condition is
![\begin{displaymath}\bgroup\color{black}k\left[{{\cos\rho\over\rho}-{\sin\rho\ove...
...}\over {e^{i\rho}\over i\rho}}\right]_{\rho=i\kappa a} .\egroup\end{displaymath}](img1896.png)