Next: Momentum Eigenfunctions Up: The Particle in a Previous: The Particle in a Contents
If we simply redefine the position of the box so that
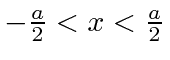 ,
then our problem has symmetry under the Parity operation.
,
then our problem has symmetry under the Parity operation.
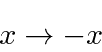
![\begin{displaymath}\bgroup\color{black}[H,P]=0 \egroup\end{displaymath}](img1158.png)
This means that
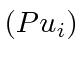 is an eigenfunction of
is an eigenfunction of
![]() with the same energy eigenvalue.
with the same energy eigenvalue.
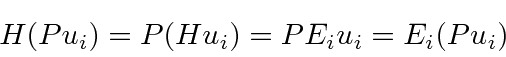
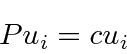
If we operate twice with parity, we get back to the original function,
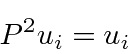
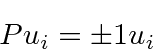
The boundary conditions are
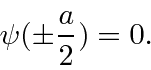
This gives two types of solutions.
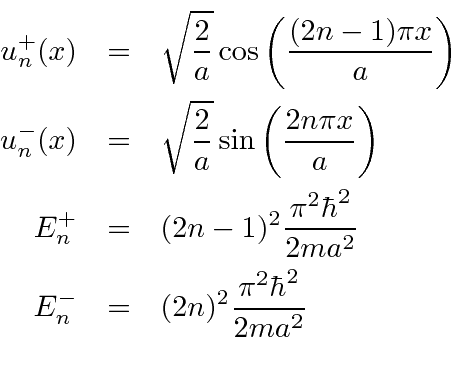
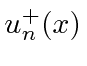 have eigenvalue +1 under the parity operator.
The
have eigenvalue +1 under the parity operator.
The
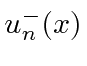 have eigenvalue -1 under the parity operator.
have eigenvalue -1 under the parity operator.
This is an example of a symmetry of the problem, causing an operator to commute
with the Hamiltonian.
We can then have simultaneous eigenfunctions of that operator and
![]() .
In this case all the energy eigenfunctions are also eigenstates of parity.
Parity is conserved.
.
In this case all the energy eigenfunctions are also eigenstates of parity.
Parity is conserved.
An arbitrary wave function can be written as a sum of the energy eigenfunctions
recovering the Fourier series in its standard form.
![\begin{displaymath}\bgroup\color{black}\psi(x)=\sum\limits_{n=1}^\infty[A_n^+ u_n^+(x)+A_n^-u_n^-(x)] \egroup\end{displaymath}](img1169.png)
Jim Branson 2013-04-22