Next: Operators Up: Wave Packets Previous: Estimate the Hydrogen Ground Contents
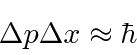
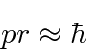
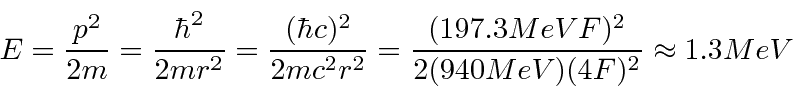
The electron energy will be higher and its rest mass is only 0.51 MeV so it WILL be relativistic.
This makes it easier.
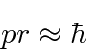
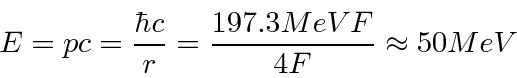
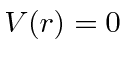 for
for 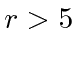 Fermis and
Fermis and 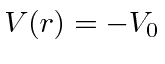 for
for 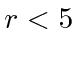 Fermis.
Use the uncertainty principle to estimate the minimum value of
Fermis.
Use the uncertainty principle to estimate the minimum value of 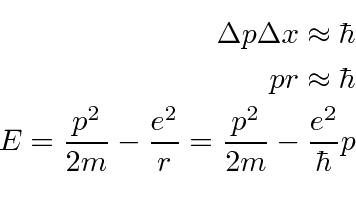
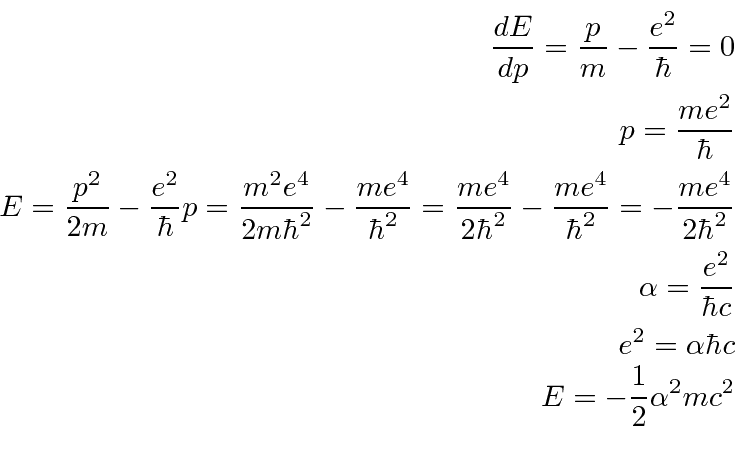
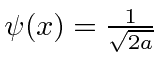 for
for 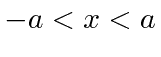 , otherwise
, otherwise 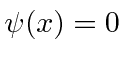 .
.
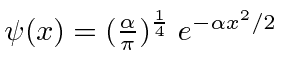
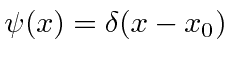
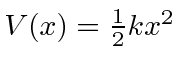 .
.
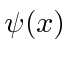 that corresponds to
that corresponds to
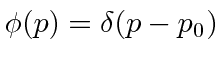 .
.
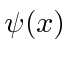 that corresponds to
that corresponds to
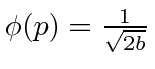 for
for 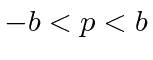 , and
, and 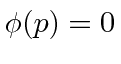 otherwise.
otherwise.
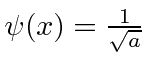 for
for 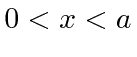 and that
and that
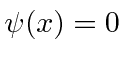 elsewhere.
What is the probability for the particle to have a momentum between
elsewhere.
What is the probability for the particle to have a momentum between 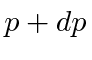 ?
?
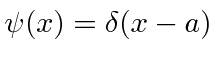 .
Find the wave-function in momentum space. Is the state correctly normalized? Explain why.
.
Find the wave-function in momentum space. Is the state correctly normalized? Explain why.
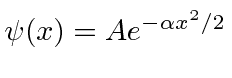 .
What is the probability for the particle to have a momentum between
.
What is the probability for the particle to have a momentum between 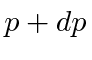 ?
?
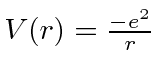 . Use the
uncertainty principle to estimate the ground state energy.
. Use the
uncertainty principle to estimate the ground state energy.
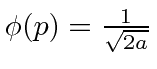 for
for 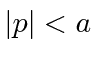 and
and 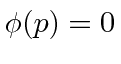 elsewhere.
What is
elsewhere.
What is 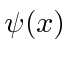 ?
What is the probability to find the particle between
?
What is the probability to find the particle between 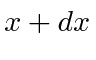 ?
?
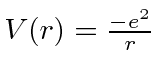 .
It is also possible to make a hydrogen-like atom from a proton and a muon.
The force binding the muon to the proton is identical to that for the electron
but the muon's mass is 106 MeV/c
.
It is also possible to make a hydrogen-like atom from a proton and a muon.
The force binding the muon to the proton is identical to that for the electron
but the muon's mass is 106 MeV/c . Show that the uncertainty
principle is satisfied.
. Show that the uncertainty
principle is satisfied.
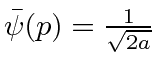 for
for 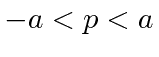 ,
,
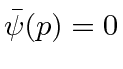 elsewhere.
elsewhere.
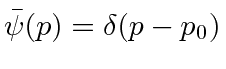
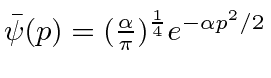
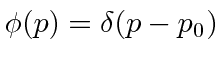 .
What is
.
What is 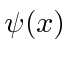 ?
What is
?
What is 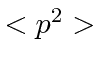 ?
What is
?
What is 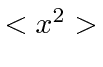 ?
?
Jim Branson 2013-04-22