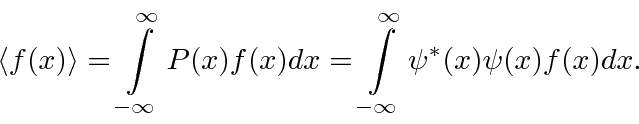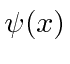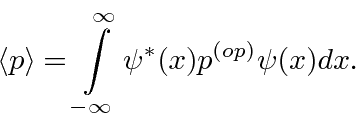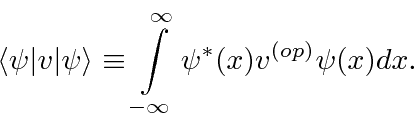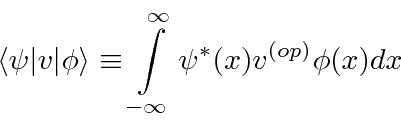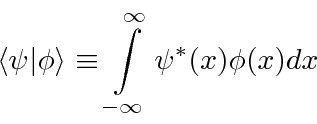We can use operators to help us compute the
expectation value
of a physical variable.
If a particle is in the state
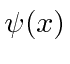 ,
the normal way to compute the expectation value of
,
the normal way to compute the expectation value of
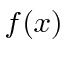 is
is
If the variable we wish to compute the expectation value of (like
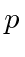 )
is not a simple function of
)
is not a simple function of
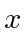 , let its operator act on
, let its operator act on
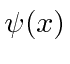
We have a shorthand notation for the expectation value of a variable
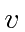 in the state
in the state
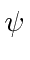 which is quite useful.
which is quite useful.
We extend the notation from just expectation values to
and
We use this shorthand
Dirac Bra-Ket notation a great deal.
Jim Branson
2013-04-22
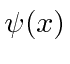 ,
the normal way to compute the expectation value of
,
the normal way to compute the expectation value of
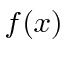 is
is