Next: Classical Scalar Field in Up: Classical Scalar Fields Previous: Classical Scalar Fields Contents
This section is a review of mechanical systems largely from the point of view of Lagrangian dynamics. In particular, we review the equations of a string as an example of a field theory in one dimension.
We start with the Lagrangian of a discrete system like a single particle.
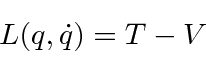
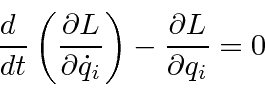
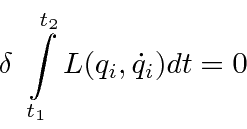
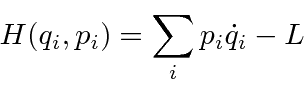
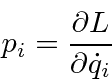
For a continuous system, like a string, the Lagrangian is an integral of a Lagrangian density function.
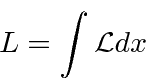
![\begin{displaymath}\bgroup\color{black} {\cal L}={1\over 2}\left[\mu\dot{\eta}^2-Y\left({\partial\eta\over\partial x}\right)^2\right] \egroup\end{displaymath}](img3762.png)
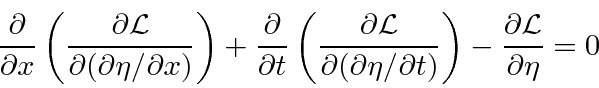
The Hamiltonian density can be computed from the Lagrangian density and is a function of the coordinate
![]() and its
conjugate momentum.
and its
conjugate momentum.
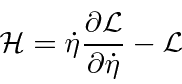
In this example of a string,
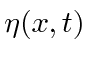 is a simple scalar field.
The string has a displacement at each point along it which varies as a function of time.
is a simple scalar field.
The string has a displacement at each point along it which varies as a function of time.
If we apply the Euler-Lagrange equation, we get a differential equation that the string's displacement will satisfy.
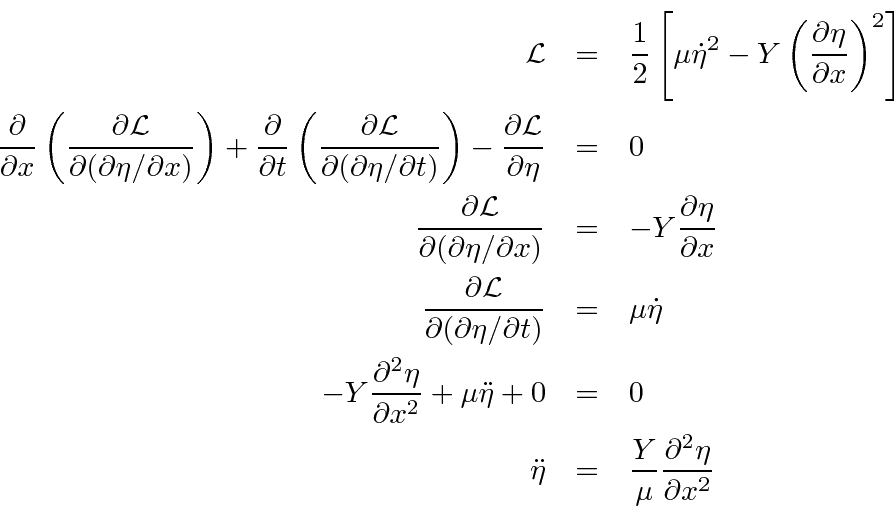
Jim Branson 2013-04-22