Next: Scattering from a Hard Up: Scattering Previous: Scattering Contents
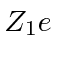 in a
screened Coulomb potential
in a
screened Coulomb potential
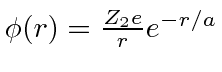 .
The exponential represents the screening of the nuclear charge by atomic electrons.
Without screening, the total Coulomb scattering cross section is infinite because the range of the force in infinite.
.
The exponential represents the screening of the nuclear charge by atomic electrons.
Without screening, the total Coulomb scattering cross section is infinite because the range of the force in infinite.
The potential energy then is
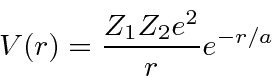
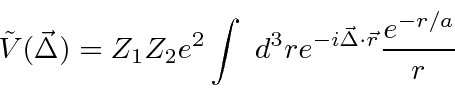
![\begin{eqnarray*}
\tilde{V}(\vec{\Delta})&=&Z_1Z_2e^2 2\pi\int\limits_0^\infty r...
...2}\right] \\
&=&{4\pi Z_1Z_2e^2\over {1\over a^2}+\Delta^2} \\
\end{eqnarray*}](img3740.png)
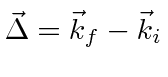 , we have
, we have
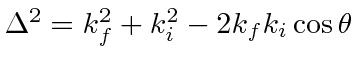 .
For elastic scattering,
.
For elastic scattering,
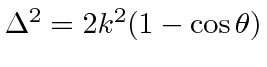 .
The differential cross section is
.
The differential cross section is
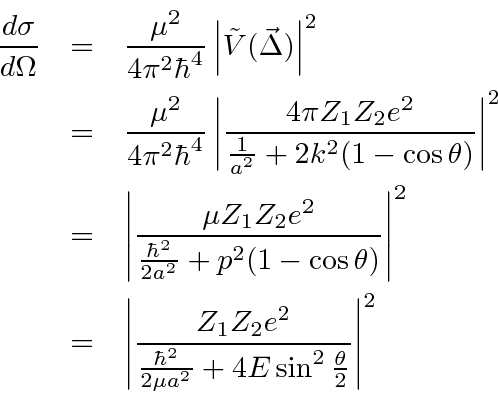
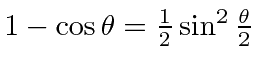 .
.
The screened Coulomb potential gives a finite total cross section.
It corresponds well with the experiment Rutherford did in which
![]() particles were scattered from atoms in a foil.
If we scatter from a bare charge where there is no screening, we can take the limit in which
particles were scattered from atoms in a foil.
If we scatter from a bare charge where there is no screening, we can take the limit in which
![]() .
.
Jim Branson 2013-04-22