Next: Homework Problems Up: Derivations and Computations Previous: Derivations and Computations Contents
![\begin{displaymath}\bgroup\color{black} P_n\propto \left[{4\sin^2\left((\omega_{ni}+\omega) t/2\right)\over (\omega_{ni}+\omega)^2}\right] \egroup\end{displaymath}](img3542.png)
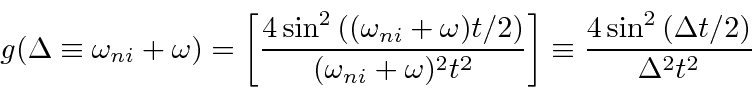
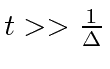 .
(Note that we have divided our function to be investigated by
.
(Note that we have divided our function to be investigated by
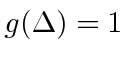 while for all other values for
while for all other values for
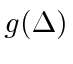 approaches zero for large
approaches zero for large
To find out exactly what delta function it is, we need to integrate over
![]() .
.
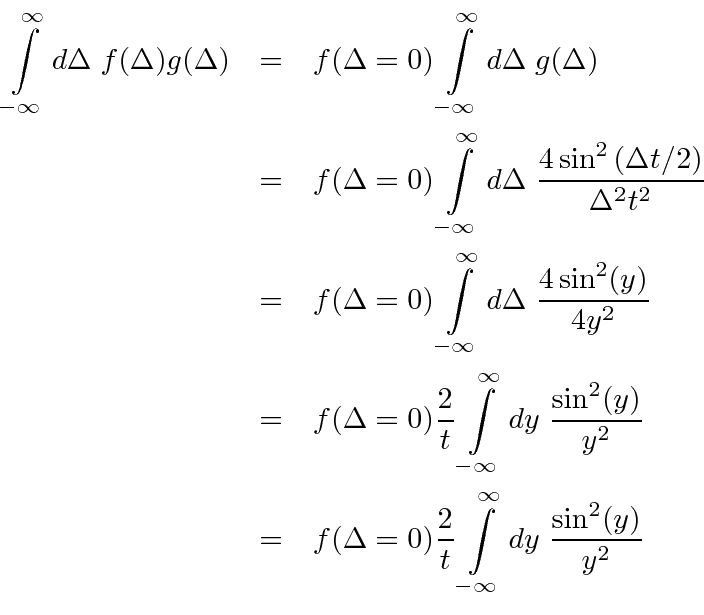
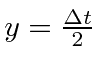 .
The definite integral over
.
The definite integral over
![\begin{eqnarray*}
\int\limits_{-\infty}^\infty d\Delta\; f(\Delta) g(\Delta) &=&...
...mega_{ni}+\omega)^2}\right]&=&2\pi t\:\delta(\omega_{ni}+\omega)
\end{eqnarray*}](img3550.png)
Jim Branson 2013-04-22