Next: The Molecule Up: Molecular Physics Previous: Molecular Physics Contents
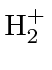 Ion
Ion
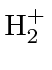 ion.
It has two nuclei (A and B) sharing one electron (1).
ion.
It has two nuclei (A and B) sharing one electron (1).
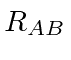 is the distance between the two nuclei.
is the distance between the two nuclei.
The lowest energy wavefunction can be thought of as a (anti)symmetric linear combination of an
electron in the ground state near nucleus A and the ground state near nucleus B
![\begin{displaymath}\bgroup\color{black}\psi_\pm\left(\vec{r},\vec{R}\right)=C_\pm(R)\left[\psi_A\pm\psi_B\right]\egroup\end{displaymath}](img370.png)
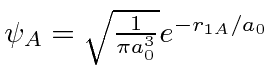 is g.s. around nucleus A.
is g.s. around nucleus A.
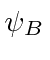 are not orthogonal; there is overlap.
We must compute the normalization constant to estimate the energy.
are not orthogonal; there is overlap.
We must compute the normalization constant to estimate the energy.
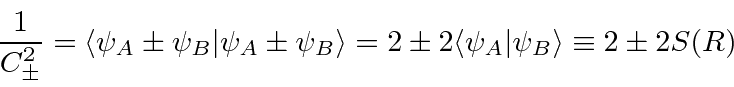
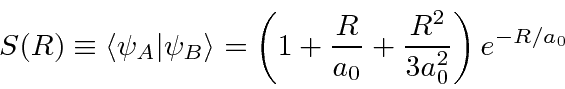
We can now compute the energy of these states.
![\begin{eqnarray*}
\left<H_0\right>_\pm &=&{1\over {2[1\pm S(R)]}}\left<\psi_A\pm...
...> \pm \left<\psi_A\vert H_0\vert\psi_B\right> \over {1\pm S(R)}}
\end{eqnarray*}](img3467.png)
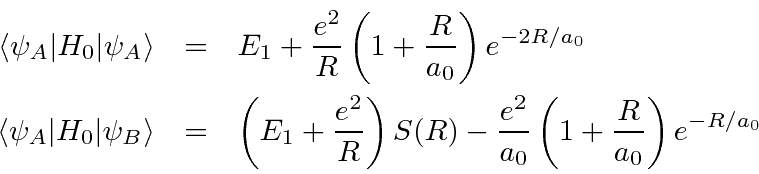
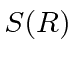 in the above.
Now, we plug these in and rewrite things in terms of
in the above.
Now, we plug these in and rewrite things in terms of
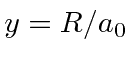 ,
the distance between the atoms in units of the Bohr radius.
,
the distance between the atoms in units of the Bohr radius.
![\begin{eqnarray*}
\left<H_0\right>_\pm &=& {E_1+{e^2\over R}\left(1+R/a_0\right)...
...2/3)e^{-y}-2(1+y)e^{-y}\right]
\over{ 1\pm (1+y+y^2/3)e^{-y}}}
\end{eqnarray*}](img3471.png)
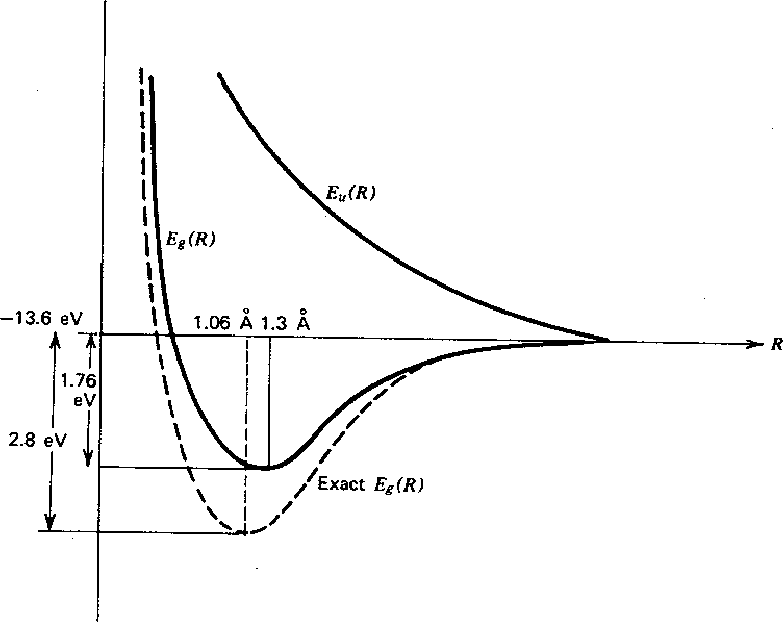
The graph below shows the energies from our calculation for the space symmetric
 and antisymmetric
and antisymmetric
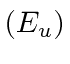 states as well as the result of a more complete calculation (Exact
states as well as the result of a more complete calculation (Exact
![]() ) as a function of the distance between
the protons
) as a function of the distance between
the protons
![]() .
Our calculation for the symmetric state shows a minimum arount 1.3 Angstroms between the nuclei and
a Binding Energy of 1.76 eV.
We could get a better estimate by introduction some parameters in our trial wave function and
using the variational method.
.
Our calculation for the symmetric state shows a minimum arount 1.3 Angstroms between the nuclei and
a Binding Energy of 1.76 eV.
We could get a better estimate by introduction some parameters in our trial wave function and
using the variational method.
The antisymmetric state shows no minimum and never goes below -13.6 eV so there is no binding in this state.
By setting
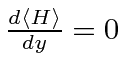 , we can get the distance between atoms and the energy.
, we can get the distance between atoms and the energy.
| Distance | Energy | |
| Calculated | 1.3 Å | -1.76 eV |
| Actual | 1.06 Å | -2.8 eV |
Its clear we would need to introduce some wfn. parameters to get good precision.
Jim Branson 2013-04-22