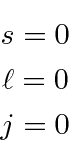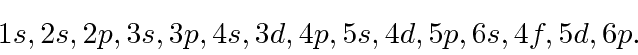The Hamiltonian for an atom with
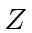 electrons and protons is
electrons and protons is
We have seen that the coulomb repulsion between electrons is a very large
correction in Helium and that the three body problem in quantum mechanics
is only solved by approximation.
The states we have from hydrogen are modified significantly.
What hope do we have to understand even more complicated atoms?
The physics of closed shells and angular momentum enable us to
make sense of even the most complex atoms.
Because of the Pauli principle, we can put only one electron into each state.
When we have enough electrons to fill a shell, say the 1s or 2p, The resulting
electron distribution is spherically symmetric because
With all the states filled and the relative phases determined by the antisymmetry
required by Pauli,
the quantum numbers of the closed shell are determined.
There is only one possible state representing a closed shell.
As in Helium, the two electrons in the same spatial state,
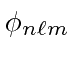 , must by symmetric in
space and hence antisymmetric in spin.
This implies each pair of electrons has a total spin of 0.
Adding these together gives a total spin state with
, must by symmetric in
space and hence antisymmetric in spin.
This implies each pair of electrons has a total spin of 0.
Adding these together gives a total spin state with
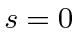 , which is antisymmetric under interchange.
The spatial state must be totally symmetric under interchange and, since all the states in the shell
have the same
, which is antisymmetric under interchange.
The spatial state must be totally symmetric under interchange and, since all the states in the shell
have the same
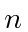 and
and
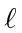 , it is the different
, it is the different
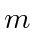 states which are symmetrized.
This can be shown to give us a total
states which are symmetrized.
This can be shown to give us a total
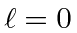 state.
state.
So the
closed shell contributes a spherically symmetric charge and spin distribution
with the quantum numbers
The closed shell screens the nuclear charge.
Because of the screening, the potential no longer has a pure
 behavior.
Electrons which are far away from the nucleus see less of the nuclear charge and shift up
in energy.
This is a large effect and single electron states with larger
behavior.
Electrons which are far away from the nucleus see less of the nuclear charge and shift up
in energy.
This is a large effect and single electron states with larger
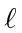 have larger energy.
From lowest to highest energy, the atomic shells have the order
have larger energy.
From lowest to highest energy, the atomic shells have the order
The effect of screening not only breaks the degeneracy between states with the same
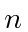 but
different
but
different
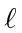 , it even moves the 6s state, for example, to have lower energy than the 4f or 5d states.
The 4s and 3d states have about the same energy in atoms because of screening.
, it even moves the 6s state, for example, to have lower energy than the 4f or 5d states.
The 4s and 3d states have about the same energy in atoms because of screening.
Jim Branson
2013-04-22
![\begin{displaymath}\bgroup\color{black}\left[ \sum\limits^Z_{i=1} \left({p^2_i\o...
...\vert\vec{r_i}-\vec{r_j}\right\vert}} \right]\psi=E\psi.\egroup\end{displaymath}](img361.png)
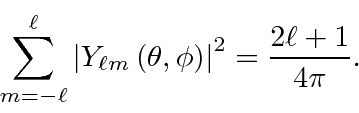
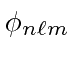 , must by symmetric in
space and hence antisymmetric in spin.
This implies each pair of electrons has a total spin of 0.
Adding these together gives a total spin state with
, must by symmetric in
space and hence antisymmetric in spin.
This implies each pair of electrons has a total spin of 0.
Adding these together gives a total spin state with
![]() , which is antisymmetric under interchange.
The spatial state must be totally symmetric under interchange and, since all the states in the shell
have the same
, which is antisymmetric under interchange.
The spatial state must be totally symmetric under interchange and, since all the states in the shell
have the same
![]() and
and
![]() , it is the different
, it is the different
![]() states which are symmetrized.
This can be shown to give us a total
states which are symmetrized.
This can be shown to give us a total
![]() state.
state.