- Calculate the energy shifts to the four hyperfine
ground states of hydrogen in a weak magnetic field. (The
field is weak enough so that the perturbation is smaller than
the hyperfine splitting.)
- Calculate the splitting for the ground state of positronium due to the
spin-spin interaction between the electron and the positron.
Try to correctly use the reduced mass where required but don't let this
detail keep you from working the problem.
- A muonic hydrogen atom (proton plus muon) is in a
relative
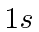 state in an external magnetic field.
Assume that the perturbation due to the hyperfine interaction and
the magnetic field is given by
state in an external magnetic field.
Assume that the perturbation due to the hyperfine interaction and
the magnetic field is given by
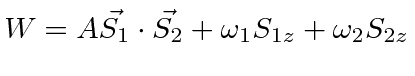 .
Calculate the energies of the four nearly degenerate ground
states.
Do not assume that any terms in the Hamiltonian are small.
.
Calculate the energies of the four nearly degenerate ground
states.
Do not assume that any terms in the Hamiltonian are small.
- A hydrogen atom in the ground state is put in a magnetic field.
Assume that the energy shift due to the B field is of the same order
as the hyperfine splitting of the ground state.
Find the eigenenergies of the (four) ground states as a function of the B field strength.
Make sure you define any constants (like
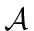 ) you use in terms of fundamental constants.
) you use in terms of fundamental constants.
Jim Branson
2013-04-22
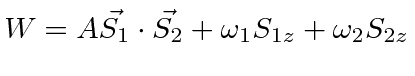 .
Calculate the energies of the four nearly degenerate ground
states.
Do not assume that any terms in the Hamiltonian are small.
.
Calculate the energies of the four nearly degenerate ground
states.
Do not assume that any terms in the Hamiltonian are small.