Hyperfine and Zeeman for H, muonium, positronium

We are able to set up the full hyperfine (plus B field) problem in a general way so that different hydrogen-like systems can be handled. We know that as the masses become more equal, the hyperfine interaction becomes more important.

Let's define our perturbation 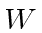$W$ as

$$\bgroup\color{black}W\equiv {{\cal A}\over\hbar^2}\vec{S}_1\cdot \vec{S}_2 + w_1S_{1z} +w_2S_{2z} \egroup$$

Here, we have three constants that are determined by the strength of the interactions. We include the interaction of the ``nuclear'' magnetic moment with the field, which we have so far neglected. This is required because the positron, for example, has a magnetic moment equal to the electron so that it could not be neglected.

$$\bgroup\color{black}\matrix{1&1\cr 1&-1\cr 1&0\cr 0&0} \left(... ... {\hbar\over 2}(w_1-w_2) & {-3{\cal A}\over 4}} \right) \egroup$$

$$\bgroup\color{black}E_3 = -{{\cal A}\over 4}+ \sqrt{\left({{\... ... 2}\right)^2 +\left({\hbar^2\over 2}(w_1-w_2)\right)^2} \egroup$$

$$\bgroup\color{black}E_4 = -{{\cal A}\over 4}- \sqrt{\left({{\... ... 2}\right)^2 +\left({\hbar^2\over 2}(w_1-w_2)\right)^2} \egroup$$

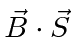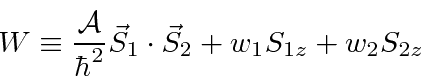
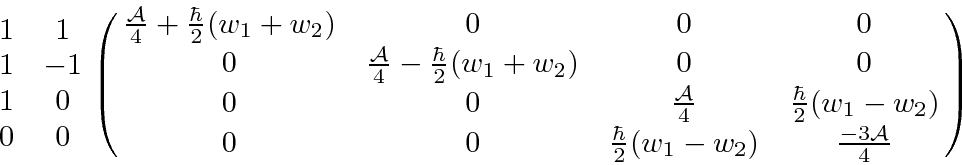
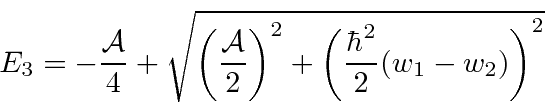
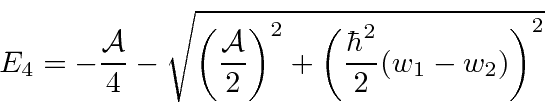
Like previous hf except now we take (proton) other $\vec{B}\cdot\vec{S}$ term into account.