Next: Hydrogen in a Strong Up: Examples Previous: Splitting of the Hydrogen Contents
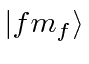 in which the hyperfine
perturbation is diagonal and compute the matrix elements for
in which the hyperfine
perturbation is diagonal and compute the matrix elements for
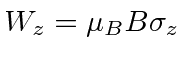 .
But to do the computation, we will have to write those states in terms of
.
But to do the computation, we will have to write those states in terms of
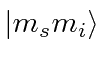 which we will abbreviate like
which we will abbreviate like
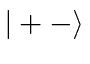 , which means the electron's spin is up and the
proton's spin is down.
, which means the electron's spin is up and the
proton's spin is down.
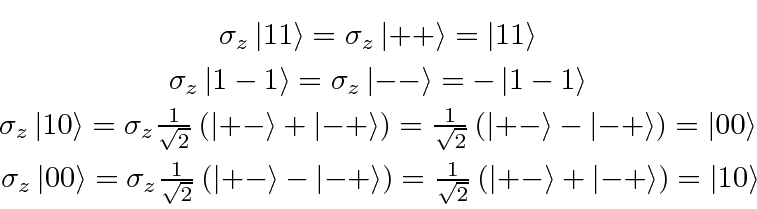
Now since the three
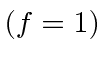 states are degenerate, we have to make sure all the
matrix elements between those states are zero, otherwise we should bite the bullet
and do the full problem as in the intermediate field case.
The
states are degenerate, we have to make sure all the
matrix elements between those states are zero, otherwise we should bite the bullet
and do the full problem as in the intermediate field case.
The
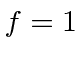 matrix is diagonal, as we could have guessed.
matrix is diagonal, as we could have guessed.
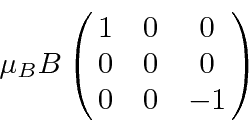
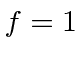 and
and
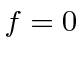 and we are
assuming the hyperfine splitting between these states is large compared to the
matrix element.
and we are
assuming the hyperfine splitting between these states is large compared to the
matrix element.
So the full answer is
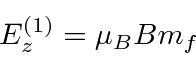
Jim Branson 2013-04-22