Next: Hyperfine Splitting in a Up: Hyperfine Structure Previous: Hyperfine Structure Contents
We can think of the nucleus as a single particle with spin
![]() .
This particle is actually made up of protons and neutrons which are
both spin
.
This particle is actually made up of protons and neutrons which are
both spin
![]() particles.
The protons and neutrons in turn are made of spin
particles.
The protons and neutrons in turn are made of spin
![]() quarks.
The magnetic dipole moment due to the nuclear spin is much smaller than
that of the electron because the mass appears in the denominator.
The magnetic moment of the nucleus is
quarks.
The magnetic dipole moment due to the nuclear spin is much smaller than
that of the electron because the mass appears in the denominator.
The magnetic moment of the nucleus is
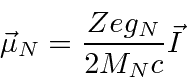
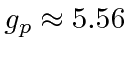 .
This is the nucleus of hydrogen upon which we will concentrate.
Even though the neutron is neutral, the gyromagnetic ratio is about -3.83.
(The quarks have gyromagnetic ratios of 2 (plus corrections) like the electron but the
problem is complicated by the strong interactions which make it hard to define a quark's mass.)
We can compute (to some accuracy) the gyromagnetic ratio of nuclei from that of protons and neutrons
as we can compute the proton's gyromagnetic ratio from its quark constituents.
.
This is the nucleus of hydrogen upon which we will concentrate.
Even though the neutron is neutral, the gyromagnetic ratio is about -3.83.
(The quarks have gyromagnetic ratios of 2 (plus corrections) like the electron but the
problem is complicated by the strong interactions which make it hard to define a quark's mass.)
We can compute (to some accuracy) the gyromagnetic ratio of nuclei from that of protons and neutrons
as we can compute the proton's gyromagnetic ratio from its quark constituents.
In any case, the nuclear dipole moment is about 1000 times smaller than that for e-spin or
![]() .
We will calculate
.
We will calculate
![]() for
for
![]() states (see Condon and Shortley for more details).
This is particularly important because it will break the degeneracy of the Hydrogen ground state.
states (see Condon and Shortley for more details).
This is particularly important because it will break the degeneracy of the Hydrogen ground state.
To get the perturbation, we should
find
![]() from
from
![]() (see Gasiorowicz page 287) then
calculate the energy change in first order perturbation theory
(see Gasiorowicz page 287) then
calculate the energy change in first order perturbation theory
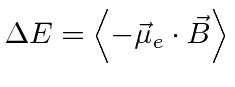 .
Calculating
the energy shift for
.
Calculating
the energy shift for
![]() states.
states.
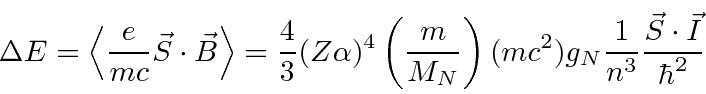
Now, just as in the case of the
![]() , spin-orbit interaction,
we will define the total angular momentum
, spin-orbit interaction,
we will define the total angular momentum
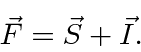
 that the hyperfine perturbation
will be diagonal.
In essence, we are doing degenerate state perturbation theory.
We could diagonalize the 4 by 4 matrix for the perturbation to solve the problem or
we can use what we know to pick the right states to start with.
Again like the spin orbit interaction, the total angular momentum states will be
the right states because we can write the perturbation in terms of
quantum numbers of those states.
that the hyperfine perturbation
will be diagonal.
In essence, we are doing degenerate state perturbation theory.
We could diagonalize the 4 by 4 matrix for the perturbation to solve the problem or
we can use what we know to pick the right states to start with.
Again like the spin orbit interaction, the total angular momentum states will be
the right states because we can write the perturbation in terms of
quantum numbers of those states.
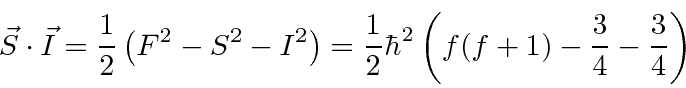
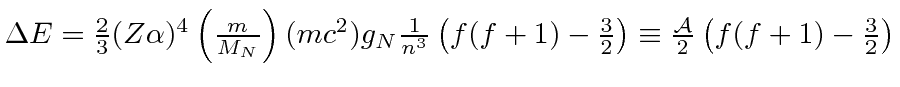 |
For the hydrogen ground state we are just adding two spin
![]() particles so the
possible values are
particles so the
possible values are
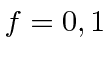 .
.
* Example:
The Hyperfine Splitting of the Hydrogen Ground State.*
The transition between the two states gives rise to EM waves with
![]() cm.
cm.
Jim Branson 2013-04-22