- The relativistic correction to the Hydrogen Hamiltonian is
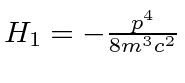 .
Assume that electrons have spin zero and that there is therefore no
spin orbit correction.
Calculate the energy shifts and draw an energy diagram for the n=3 states
of Hydrogen.
You may use
.
Assume that electrons have spin zero and that there is therefore no
spin orbit correction.
Calculate the energy shifts and draw an energy diagram for the n=3 states
of Hydrogen.
You may use
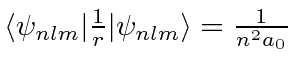 and
and
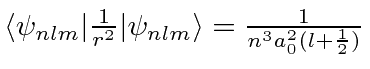 .
.
- Calculate the fine structure energy shifts (in eV!)
for the
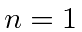 ,
, 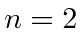 , and
, and 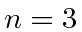 states of Hydrogen.
Include the effects of relativistic corrections, the spin-orbit interaction, and the so-called
Darwin term (due to Dirac equation). Do not include hyperfine splitting or
the effects of an external magnetic field. (Note: I am not asking you to derive the
equations.) Clearly list the states in spectroscopic notation and make a diagram showing the
allowed electric dipole decays of these states.
states of Hydrogen.
Include the effects of relativistic corrections, the spin-orbit interaction, and the so-called
Darwin term (due to Dirac equation). Do not include hyperfine splitting or
the effects of an external magnetic field. (Note: I am not asking you to derive the
equations.) Clearly list the states in spectroscopic notation and make a diagram showing the
allowed electric dipole decays of these states.
- Calculate and show the splitting of the
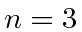 states (as in the previous problem)
in a weak magnetic field B. Draw a diagram showing the states before and after the
field is applied
states (as in the previous problem)
in a weak magnetic field B. Draw a diagram showing the states before and after the
field is applied
- If the general form of the spin-orbit coupling for a particle of
mass
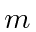 and spin
and spin 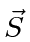 moving in a potential
moving in a potential 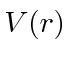 is
is
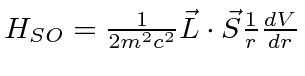 ,
what is the effect of that coupling on the spectrum of an
electron bound in a 3D harmonic oscillator?
Give the energy shifts and and draw a diagram for the
,
what is the effect of that coupling on the spectrum of an
electron bound in a 3D harmonic oscillator?
Give the energy shifts and and draw a diagram for the  and
and 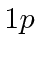 states.
states.
for the 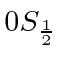 ,
, 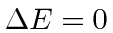 ,
,
for the 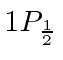 ,
,
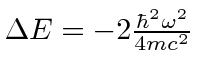 ,
,
for the 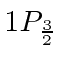 ,
,
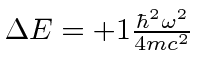 .
.
- We computed that the
energies after the fine structure corrections to the hydrogen
spectrum are
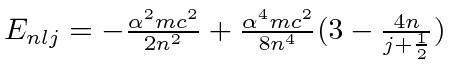 .
Now a weak magnetic field
.
Now a weak magnetic field 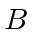 is applied to hydrogen atoms
in the
is applied to hydrogen atoms
in the 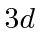 state.
Calculate the energies of all the
state.
Calculate the energies of all the 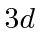 states (ignoring hyperfine
effects).
Draw an energy level diagram, showing the quantum numbers of
the states and the energy splittings.
states (ignoring hyperfine
effects).
Draw an energy level diagram, showing the quantum numbers of
the states and the energy splittings.
- In Hydrogen, the
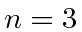 state is split by fine structure corrections into states of
definite
state is split by fine structure corrections into states of
definite 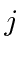 ,
,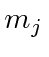 ,
,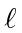 , and
, and 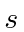 .
According to our calculations of the fine structure, the energy only depends on
.
According to our calculations of the fine structure, the energy only depends on 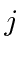 .
We label these states in spectroscopic notation:
.
We label these states in spectroscopic notation: 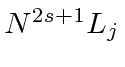 .
Draw an energy diagram for the
.
Draw an energy diagram for the 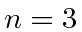 states, labeling each state in spectroscopic notation.
Give the energy shift due to the fine structure corrections in units of
states, labeling each state in spectroscopic notation.
Give the energy shift due to the fine structure corrections in units of 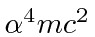 .
.
- The energies of photons emitted in the Hydrogen atom
transition between the 3S and the 2P states are measured, first with
no external field, then, with the atoms in a uniform magnetic field B.
Explain in detail the spectrum of photons before and after the field
is applied. Be sure to give an expression for any relevant energy
differences.
Jim Branson
2013-04-22
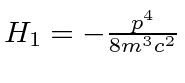 .
Assume that electrons have spin zero and that there is therefore no
spin orbit correction.
Calculate the energy shifts and draw an energy diagram for the n=3 states
of Hydrogen.
You may use
.
Assume that electrons have spin zero and that there is therefore no
spin orbit correction.
Calculate the energy shifts and draw an energy diagram for the n=3 states
of Hydrogen.
You may use
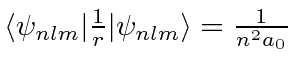 and
and
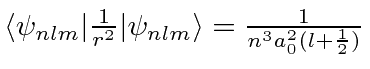 .
.
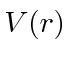 is
is
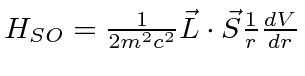 ,
what is the effect of that coupling on the spectrum of an
electron bound in a 3D harmonic oscillator?
Give the energy shifts and and draw a diagram for the
,
what is the effect of that coupling on the spectrum of an
electron bound in a 3D harmonic oscillator?
Give the energy shifts and and draw a diagram for the ![\begin{eqnarray*}
& V={1\over 2}m\omega^2r^2 \\
& {dV\over dr}=m\omega^2 r \\
...
...O}\rangle={\hbar^2\omega^2\over 4mc^2}[j(j+1)-l(l+1)-s(s+1)] \\
\end{eqnarray*}](img3145.png)
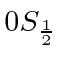 ,
, 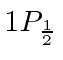 ,
,
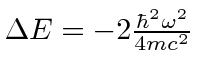 ,
,
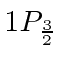 ,
,
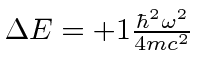 .
.
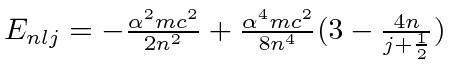 .
Now a weak magnetic field
.
Now a weak magnetic field 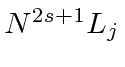 .
Draw an energy diagram for the
.
Draw an energy diagram for the