- A general one dimensional scattering problem could be characterized by an (arbitrary) potential
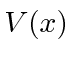 which is localized by the requirement that
which is localized by the requirement that 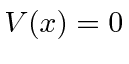 for
for 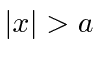 .
Assume that the wave-function is
.
Assume that the wave-function is
Relating the ``outgoing'' waves to the ``incoming'' waves by the matrix equation
show that
Use this to show that the 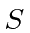 matrix is unitary.
matrix is unitary.
- Calculate the
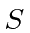 matrix for the potential
matrix for the potential
and show that the above conditions are satisfied.
- The odd bound state solution to the potential well problem bears many similarities to the zero angular momentum
solution to the 3D spherical potential well.
Assume the range of the potential is
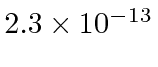 cm, the binding energy is -2.9 MeV,
and the mass of the particle is 940 MeV.
Find the depth of the potential in MeV.
(The equation to solve is transcendental.)
cm, the binding energy is -2.9 MeV,
and the mass of the particle is 940 MeV.
Find the depth of the potential in MeV.
(The equation to solve is transcendental.)
- Find the three lowest energy wave-functions for the harmonic oscillator.
- Assume the potential for particle bound inside a nucleus is given by
and that the particle has mass 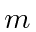 and energy
and energy 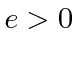 .
Estimate the lifetime of the particle inside this potential.
.
Estimate the lifetime of the particle inside this potential.
Jim Branson
2013-04-22
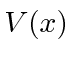 which is localized by the requirement that
which is localized by the requirement that 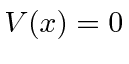 for
for 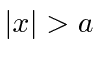 .
Assume that the wave-function is
.
Assume that the wave-function is
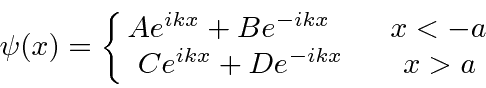
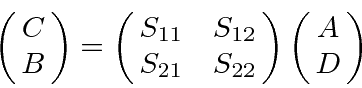
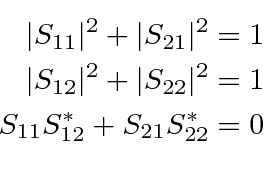
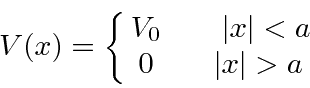
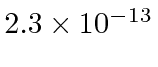 cm, the binding energy is -2.9 MeV,
and the mass of the particle is 940 MeV.
Find the depth of the potential in MeV.
(The equation to solve is transcendental.)
cm, the binding energy is -2.9 MeV,
and the mass of the particle is 940 MeV.
Find the depth of the potential in MeV.
(The equation to solve is transcendental.)
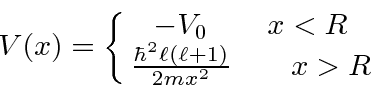
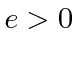 .
Estimate the lifetime of the particle inside this potential.
.
Estimate the lifetime of the particle inside this potential.