- A polished Aluminum plate is hit by beams of photons of known energy.
It is measured that the maximum electron energy is
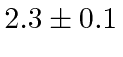 eV for
2000 Angstrom light and
eV for
2000 Angstrom light and 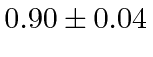 eV for 2580 Angstrom light.
Determine Planck's constant and its error based on these measurements.
eV for 2580 Angstrom light.
Determine Planck's constant and its error based on these measurements.
- A 200 keV photon collides with an electron initially at rest.
The photon is observed to scatter at 90 degrees in the electron rest frame.
What are the kinetic energies of the electron and photon after the scattering?
- Use the energy density in a cavity as a function of frequency and T
to calculate the emissive power of a black body 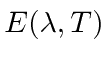 as a function of wavelength and temperature.
as a function of wavelength and temperature.
- What is the DeBroglie wavelength for each of the following particles?
The energies given are the kinetic energies.
- a 1 eV electron
- a
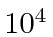 MeV proton
MeV proton
- a 1 gram lead ball moving with a velocity of 100 cm/sec.
- The Dirac delta function has the property that
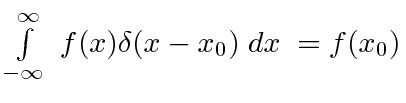 Find the momentum space wave function
Find the momentum space wave function 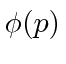 if
if
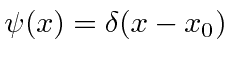 .
.
- Use the calculation of a spreading Gaussian wave packet to find the fractional change
in size of a wave packet between
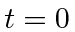 and
and 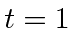 second for an electron localized to 1 Angstrom.
Now find the fraction change for a 1 gram weight localized to 1 nanometer.
second for an electron localized to 1 Angstrom.
Now find the fraction change for a 1 gram weight localized to 1 nanometer.
- Use the uncertainty principle to estimate the energy of the ground state of a harmonic
oscillator with the Hamiltonian
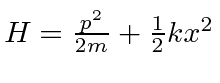 .
.
- Estimate the kinetic energy of an electron confined to be inside a nucleus of radius
5 Fermis. Estimate the kinetic energy of a neutron confined inside the same nucleus.
Jim Branson
2013-04-22
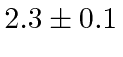 eV for
2000 Angstrom light and
eV for
2000 Angstrom light and 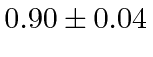 eV for 2580 Angstrom light.
Determine Planck's constant and its error based on these measurements.
eV for 2580 Angstrom light.
Determine Planck's constant and its error based on these measurements.
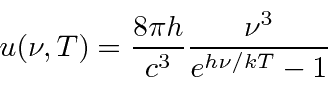
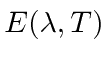 as a function of wavelength and temperature.
as a function of wavelength and temperature.
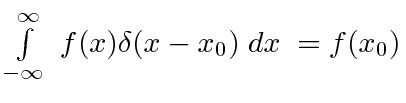 Find the momentum space wave function
Find the momentum space wave function 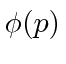 if
if
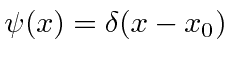 .
.
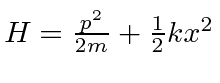 .
.