The pseudo-potential dominates the behavior of the wavefunction at the originif the potential is less singular than
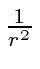 .
.
For small
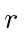 , the equation becomes
, the equation becomes
The dominant term at the origin will be given by some power of
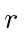
Higher powers of
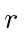 are OK, but are not dominant.
Plugging this into the equation we get
are OK, but are not dominant.
Plugging this into the equation we get
There are actually two solutions to this equation,
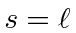 and
and
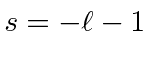 .
The first solution,
.
The first solution,
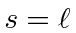 , is well behaved at the origin (regular solution).
The second solution,
, is well behaved at the origin (regular solution).
The second solution,
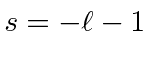 , causes normalization problems at the origin
(irregular solution).
, causes normalization problems at the origin
(irregular solution).
Jim Branson
2013-04-22
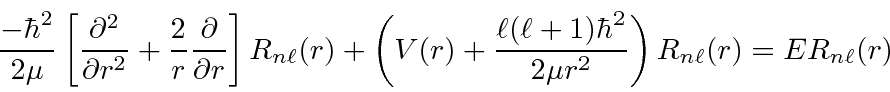
![\begin{displaymath}\bgroup\color{black}\left[{\partial^2\over\partial r^2}+{2\ov...
...ght]R_{n\ell}(r)
-{\ell(\ell+1)\over r^2}R_{n\ell}(r)=0 \egroup\end{displaymath}](img1858.png)
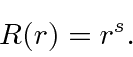
![\begin{displaymath}\bgroup\color{black}\left[s(s-1)r^{s-2}+2sr^{s-2}\right]-\ell(\ell+1)r^{s-2}=0. \egroup\end{displaymath}](img1860.png)
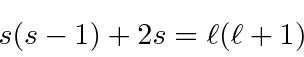
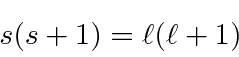
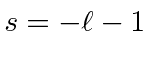 .
The first solution,
.
The first solution,
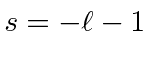 , causes normalization problems at the origin
(irregular solution).
, causes normalization problems at the origin
(irregular solution).