- Derive the commutators
![$[L^2,L_+]$](img1804.png) and
and ![$[L_z,L_+]$](img1805.png) .
Now show that
.
Now show that
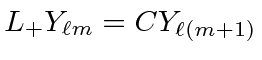 , that is,
, that is,
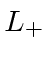 raises the
raises the 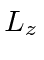 eigenvalue but does not change the
eigenvalue but does not change the 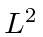 eigenvalue.
eigenvalue.
Answer
Since 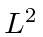 commutes with both
commutes with both 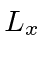 and
and 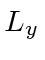 ,
,
We have the commutators. Now we apply them to a 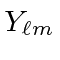 .
.
So, 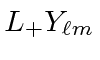 is also an eigenfunction of
is also an eigenfunction of 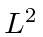 with the same eigenvalue.
with the same eigenvalue.
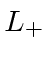 does not change
does not change 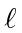 .
.
So, 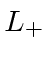 raises the eigenvalue of
raises the eigenvalue of 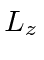 .
.
- Write the (normalized) state which is an eigenstate of
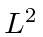 with eigenvalue
with eigenvalue
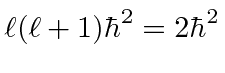 and also
an eigenstate of
and also
an eigenstate of 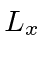 with eigenvalue
with eigenvalue 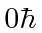 in terms of the usual
in terms of the usual 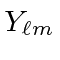 .
.
Answer
An eigenvalue of
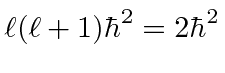 implies
implies 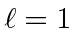 .
We will need a linear combination of the
.
We will need a linear combination of the 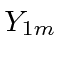 to get the eigenstate of
to get the eigenstate of
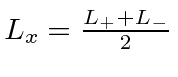 .
.
Since this is true for all  and
and 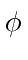 , each term must be zero.
, each term must be zero.
The state is
The trivial solution that 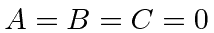 is just a zero state, not normalizable to 1.
is just a zero state, not normalizable to 1.
- Write the (normalized) state which is an eigenstate of
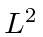 with eigenvalue
with eigenvalue
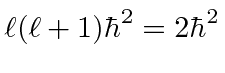 and also
an eigenstate of
and also
an eigenstate of 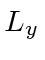 with eigenvalue
with eigenvalue 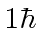 in terms of the usual
in terms of the usual 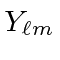 .
.
- Calculate the commutators
![$[p_z,L_x]$](img1832.png) and
and ![$[L_x^2,L_z]$](img1833.png) .
.
- Derive the relation
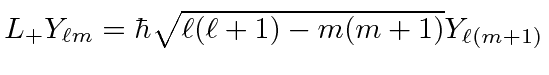 .
.
- A particle is in a
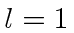 state and is known to have angular momentum
in the
state and is known to have angular momentum
in the 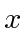 direction equal to
direction equal to 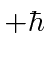 . That is
. That is
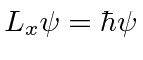 .
Since we know
.
Since we know 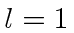 ,
, 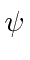 must have the form
must have the form
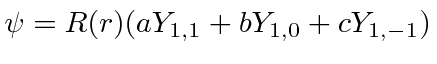 .
Find the coefficients
.
Find the coefficients 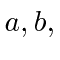 and
and 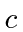 for
for 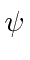 normalized.
normalized.
- Calculate the following commutators:
![$[x,L_z]$](img1841.png) ,
, ![$[L_+,L^2]$](img1842.png) ,
,
![$[{1\over 2}m\omega^2r^2,p_x]$](img1843.png) .
.
- Prove that, if the Hamiltonian is symmetric under rotations,
then
![$[H,L_z]=0$](img1844.png) .
.
- In 3 dimensions, a particle is in the state:
where 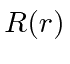 is some arbitrary radial wave function normalized such that
is some arbitrary radial wave function normalized such that
- a)
- Find the value of C that will normalize this wave function.
- b)
- If a measurement of
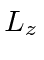 is made, what are the possible measured
values and what are probabilities for each.
is made, what are the possible measured
values and what are probabilities for each.
- c)
- Find the expected value of
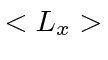 in the above state.
in the above state.
- Two (different) atoms of masses
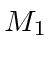 and
and 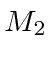 are bound
together into the ground state of a diatomic molecule.
The binding is such that radial excitations can be neglected
at low energy and that the atoms can be assumed to be a constant
distance
are bound
together into the ground state of a diatomic molecule.
The binding is such that radial excitations can be neglected
at low energy and that the atoms can be assumed to be a constant
distance 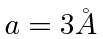 apart. (We will ignore the small spread around
apart. (We will ignore the small spread around 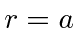 .)
.)
- a)
- What is the energy spectrum due to rotations of the molecule?
- b)
- Assuming that
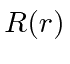 is given, write down the energy
eigenfunctions for the ground state and the first excited state.
is given, write down the energy
eigenfunctions for the ground state and the first excited state.
- c)
- Assuming that both masses are about 1000 MeV,
how does the excitation energy of the first excited state
compare to thermal energies at
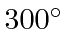 K.
K.
Jim Branson
2013-04-22
![$[L^2,L_+]$](img1804.png) and
and ![$[L_z,L_+]$](img1805.png) .
Now show that
.
Now show that
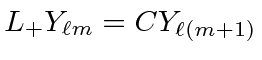 , that is,
, that is,
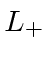 raises the
raises the 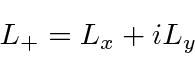
![\begin{displaymath}[L^2,L_+]=0 .\end{displaymath}](img1809.png)
![\begin{displaymath}[L_z,L_+]=[L_z,L_x+iL_y]=[L_z,L_x]+i[L_z,L_y]=i\hbar(L_y-iL_x)=\hbar(L_x+iL_y)=\hbar L_+ \end{displaymath}](img1810.png)
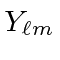 .
.
![\begin{displaymath}[L^2,L_+]Y_{\ell m}=L^2L_+Y_{\ell m}-L_+L^2Y_{\ell m}=0 \end{displaymath}](img1812.png)
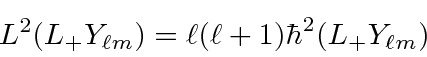
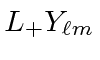 is also an eigenfunction of
is also an eigenfunction of 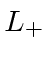 does not change
does not change ![\begin{displaymath}[L_z,L_+]Y_{\ell m}=L_zL_+Y_{\ell m}-L_+L_zY_{\ell m}=\hbar L_+Y_{\ell m} \end{displaymath}](img1815.png)
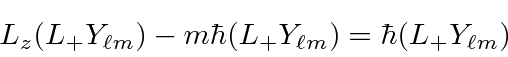
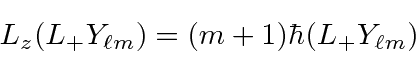
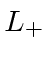 raises the eigenvalue of
raises the eigenvalue of 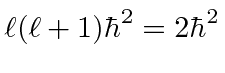 and also
an eigenstate of
and also
an eigenstate of 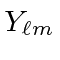 .
.
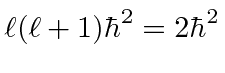 implies
implies 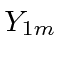 to get the eigenstate of
to get the eigenstate of
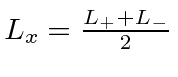 .
.
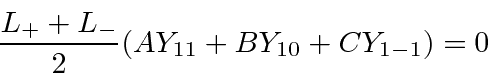
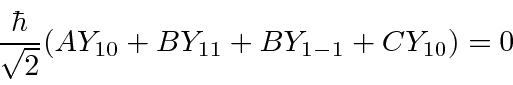
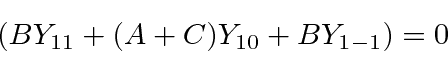
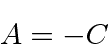
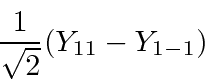
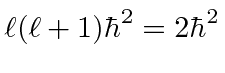 and also
an eigenstate of
and also
an eigenstate of 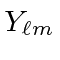 .
.
![$[p_z,L_x]$](img1832.png) and
and ![$[L_x^2,L_z]$](img1833.png) .
.
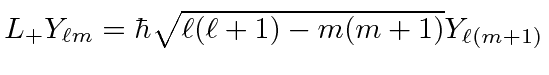 .
.
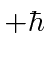 . That is
. That is
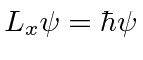 .
Since we know
.
Since we know 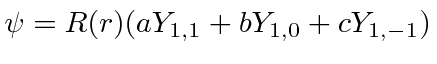 .
Find the coefficients
.
Find the coefficients 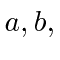 and
and ![$[x,L_z]$](img1841.png) ,
, ![$[L_+,L^2]$](img1842.png) ,
,
![$[{1\over 2}m\omega^2r^2,p_x]$](img1843.png) .
.
![$[H,L_z]=0$](img1844.png) .
.
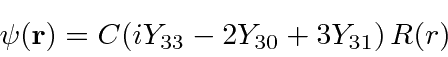
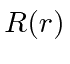 is some arbitrary radial wave function normalized such that
is some arbitrary radial wave function normalized such that
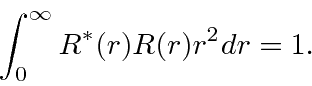
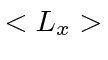 in the above state.
in the above state.
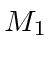 and
and 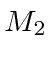 are bound
together into the ground state of a diatomic molecule.
The binding is such that radial excitations can be neglected
at low energy and that the atoms can be assumed to be a constant
distance
are bound
together into the ground state of a diatomic molecule.
The binding is such that radial excitations can be neglected
at low energy and that the atoms can be assumed to be a constant
distance 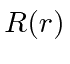 is given, write down the energy
eigenfunctions for the ground state and the first excited state.
is given, write down the energy
eigenfunctions for the ground state and the first excited state.