Next: Derivations and Computations Up: The Angular Momentum Eigenfunctions Previous: The Angular Momentum Eigenfunctions Contents
In spherical coordinates, the parity operation is
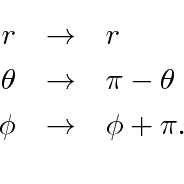
The radial part of the wavefunction, therefore, is unchanged and the
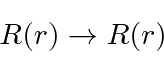
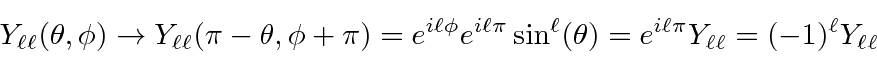
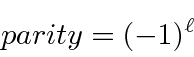
The angular momentum operators are axial vectors and do not change sign under a parity
transformation.
Therefore,
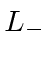 does not change under parity and all the
does not change under parity and all the
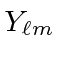 with have the
same parity as
with have the
same parity as
![]()
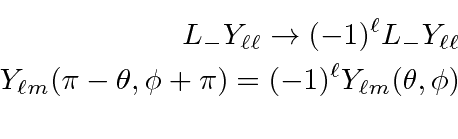
Jim Branson 2013-04-22