Next: Projection Operators and Completeness Up: Operators in a Vector Previous: Operators in a Vector Contents
First, a little review.
Recall that the square integrable functions form a vector space,
much like the familiar 3D vector space.
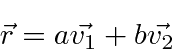
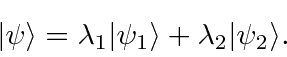
The scalar product is defined as
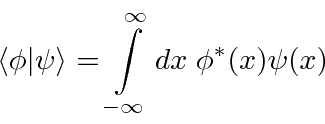
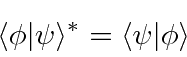
As in 3D space,
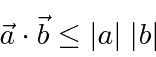
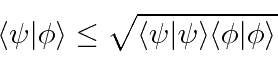
Operators are associative but not commutative.
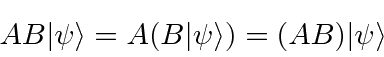
An operator transforms one vector into another vector.
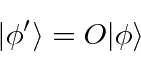
Eigenfunctions of Hermitian operators
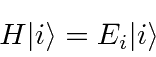
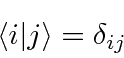
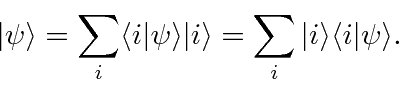
Expanding the vectors
![]() and
and
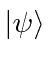 ,
,
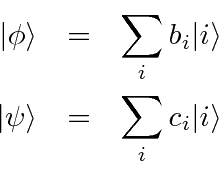
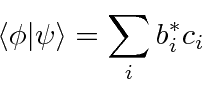
The expansion in energy eigenfunctions is a very nice way to do the
time development of a wave function.
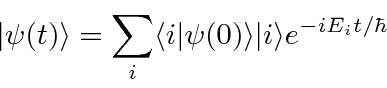
The basis of definite momentum states is not in the vector space,
yet we can use this basis to form any state in the vector space.
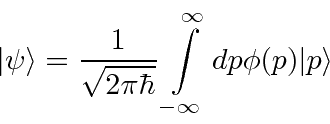
Any of these amplitudes can be used to define the state.
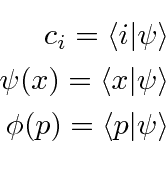
Jim Branson 2013-04-22