- A particle is confined to a box of length
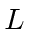 in one dimension.
It is initially in the ground state.
Suddenly, one wall of the box is moved outward making a new box of length
in one dimension.
It is initially in the ground state.
Suddenly, one wall of the box is moved outward making a new box of length 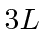 .
What is the probability that the particle is in the ground state of the new box?
You may find it useful to know that
.
What is the probability that the particle is in the ground state of the new box?
You may find it useful to know that
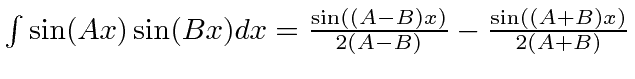
Answer
- A particle of mass
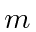 is in a 1 dimensional box of length L.
The particle is in the ground state.
The size of the box is suddenly (symmetrically) expanded to length 3L.
Find the probability for the particle to be in the ground state of the
new potential. (Your answer may include an integral which you need not
evaluate.) Find the probability to be in the first excited state of the
new potential.
is in a 1 dimensional box of length L.
The particle is in the ground state.
The size of the box is suddenly (symmetrically) expanded to length 3L.
Find the probability for the particle to be in the ground state of the
new potential. (Your answer may include an integral which you need not
evaluate.) Find the probability to be in the first excited state of the
new potential.
- Two degenerate eigenfunctions of the Hamiltonian are properly
normalized and have the following properties.
What are the properly normalized states that are eigenfunctions
of H and P?
What are their energies?
- Find the first (lowest) three Energy eigenstates for a particle localized in a box
such that
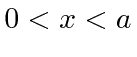 .
That is, the potential is zero inside the box and infinite outside.
State the boundary conditions and show that your solutions satisfy them.
Normalize the solutions to represent one particle in the box.
.
That is, the potential is zero inside the box and infinite outside.
State the boundary conditions and show that your solutions satisfy them.
Normalize the solutions to represent one particle in the box.
- A particle is in the first excited state of a box of length
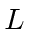 .
What is that state?
Now one wall of the box is suddenly moved outward so that the new box
has length
.
What is that state?
Now one wall of the box is suddenly moved outward so that the new box
has length 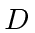 .
What is the probability for the particle to be in the ground state of the new box?
What is the probability for the particle to be in the first excited state of the new box?
.
What is the probability for the particle to be in the ground state of the new box?
What is the probability for the particle to be in the first excited state of the new box?
- *
Assume that
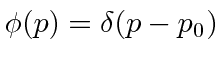 .
What is
.
What is 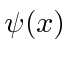 ?
What is
?
What is 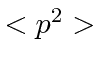 ?
What is
?
What is 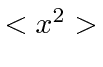 ?
?
- For a free particle, the Hamiltonian operator H is given by
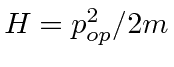 .
Find the functions,
.
Find the functions, 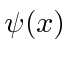 , which are eigenfunction of both the
Hamiltonian and of
, which are eigenfunction of both the
Hamiltonian and of 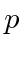 .
Write the eigenfunction that has energy eigenvalue
.
Write the eigenfunction that has energy eigenvalue 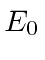 and momentum
eigenvalue
and momentum
eigenvalue 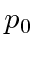 .
Now write the corresponding eigenfunctions in momentum space.
.
Now write the corresponding eigenfunctions in momentum space.
- *
A particle of mass
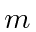 is in a 1 dimensional box of length L.
The particle is in the ground state.
A measurement is made of the particle's momentum.
Find the probability that the value measured is between
is in a 1 dimensional box of length L.
The particle is in the ground state.
A measurement is made of the particle's momentum.
Find the probability that the value measured is between 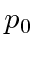 and
and 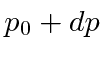 .
.
- A particle of mass
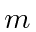 is in a constant potential
is in a constant potential 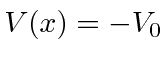 for all x. What two operators commute with the Hamiltonian and can therefore
be made constants of the motion? Since these two operators do not commute
with each other, there must be two ways to write the energy eigenfunctions, one
corresponding to each commuting operator.
Write down these two forms of the eigenfunctions of the
Hamiltonian that are also eigenfunctions of these two operators.
for all x. What two operators commute with the Hamiltonian and can therefore
be made constants of the motion? Since these two operators do not commute
with each other, there must be two ways to write the energy eigenfunctions, one
corresponding to each commuting operator.
Write down these two forms of the eigenfunctions of the
Hamiltonian that are also eigenfunctions of these two operators.
- A particle is confined to a "box" in one dimension. That is the potential is
zero for
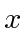 between 0 and
between 0 and 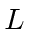 , and the potential is infinite for
, and the potential is infinite for 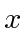 less than
zero or
less than
zero or 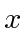 greater than
greater than 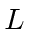 .
.
- a)
- Give an expression for the eigenfunctions of the
Hamiltonian operator. These are the time independent solutions of this
problem. (Hint: Real functions will be simplest to use here.)
- b)
- Assume that a particle is in the ground state of this box. Now
one wall of the box is suddenly moved from
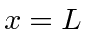 to
to 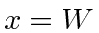 where
where 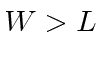 .
What is the probability that the particle is found in the ground state of the
new potential? (You may leave your answer in the form containing a clearly
specified integral.)
.
What is the probability that the particle is found in the ground state of the
new potential? (You may leave your answer in the form containing a clearly
specified integral.)
- A particle of mass
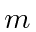 is in a 1 dimensional box of length
is in a 1 dimensional box of length 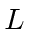 .
The particle is in the ground state.
The size of the box is suddenly expanded to length
.
The particle is in the ground state.
The size of the box is suddenly expanded to length 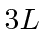 .
Find the probability for the particle to be in the ground state of the
new potential. (Your answer may include an integral which you need not
evaluate.) Find the probability to be in the first excited state of the
new potential.
.
Find the probability for the particle to be in the ground state of the
new potential. (Your answer may include an integral which you need not
evaluate.) Find the probability to be in the first excited state of the
new potential.
Jim Branson
2013-04-22
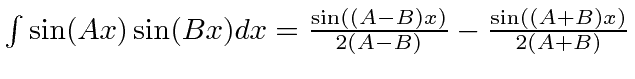
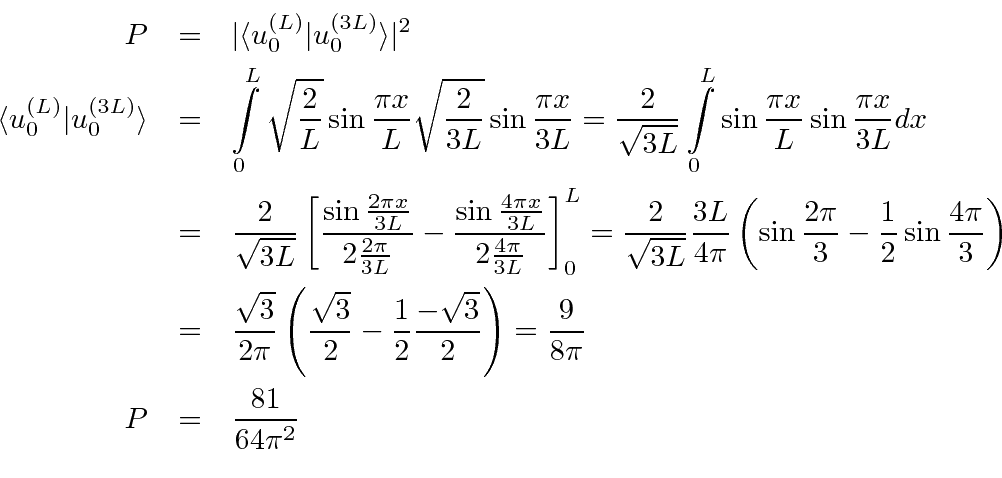
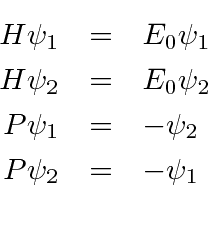
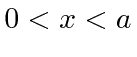 .
That is, the potential is zero inside the box and infinite outside.
State the boundary conditions and show that your solutions satisfy them.
Normalize the solutions to represent one particle in the box.
.
That is, the potential is zero inside the box and infinite outside.
State the boundary conditions and show that your solutions satisfy them.
Normalize the solutions to represent one particle in the box.
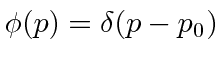 .
What is
.
What is 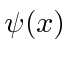 ?
What is
?
What is 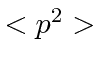 ?
What is
?
What is 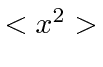 ?
?
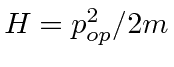 .
Find the functions,
.
Find the functions, 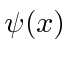 , which are eigenfunction of both the
Hamiltonian and of
, which are eigenfunction of both the
Hamiltonian and of 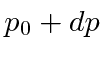 .
.
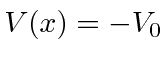 for all x. What two operators commute with the Hamiltonian and can therefore
be made constants of the motion? Since these two operators do not commute
with each other, there must be two ways to write the energy eigenfunctions, one
corresponding to each commuting operator.
Write down these two forms of the eigenfunctions of the
Hamiltonian that are also eigenfunctions of these two operators.
for all x. What two operators commute with the Hamiltonian and can therefore
be made constants of the motion? Since these two operators do not commute
with each other, there must be two ways to write the energy eigenfunctions, one
corresponding to each commuting operator.
Write down these two forms of the eigenfunctions of the
Hamiltonian that are also eigenfunctions of these two operators.
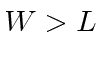 .
What is the probability that the particle is found in the ground state of the
new potential? (You may leave your answer in the form containing a clearly
specified integral.)
.
What is the probability that the particle is found in the ground state of the
new potential? (You may leave your answer in the form containing a clearly
specified integral.)