The Hamiltonian Operator

We can develop other operators using the basic ones. We will use the Hamiltonian operatorwhich, for our purposes, is the sum of the kinetic and potential energies. This is the non-relativistic case.

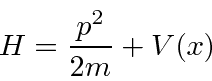
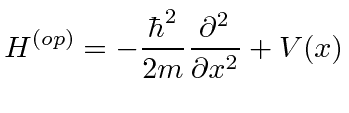$$\bgroup\color{black} H={p^2\over 2m} + V(x) \egroup$$

$$H^{(op)}=-{\hbar^2\over 2m}{\partial^2\over \partial x^2}+V(x)$$

Since the potential energy just depends on $x$, its easy to use. Angular momentum operators will later be simply computed from position and momentum operators.