Next: The Energy Operator Up: Operators in Position Space Previous: Operators in Position Space Contents
We determine the momentum operator by requiring that,
when we operate with
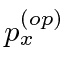 on
on
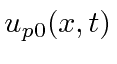 ,
we get
,
we get
![]() times the same wave function.
times the same wave function.
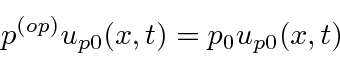
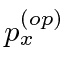 is the same as multiplying
by the variable
is the same as multiplying
by the variable
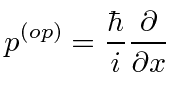 |
If we take our momentum operator and act on a arbitrary state,
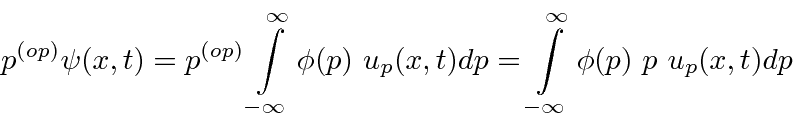
Jim Branson 2013-04-22