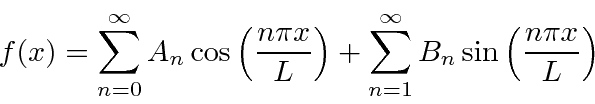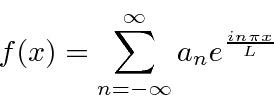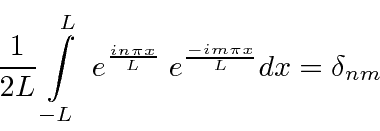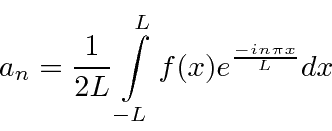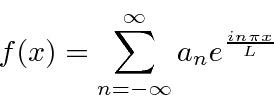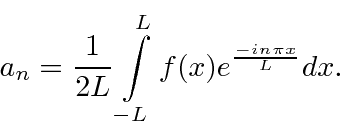Fourier Series *
Fourier series allow us to expand any periodic function on the range
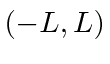 ,
in terms of sines and cosines also periodic on that interval.
,
in terms of sines and cosines also periodic on that interval.
Since the sines and cosines can be made from the complex exponentials, we can equally well use them for our basis for expansion.
This has the nice simplification of having only one term in the sum, using negative
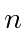 to get the other term.
to get the other term.
The exponentials are orthogonal and normalized over the interval (as were the sines and cosines)
so that we can easily compute the coefficients.
In summary, the Fourier series equations we will use are
and
We will expand the interval to infinity.
Jim Branson
2013-04-22
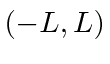 ,
in terms of sines and cosines also periodic on that interval.
,
in terms of sines and cosines also periodic on that interval.