Next: The Heisenberg Uncertainty Principle Up: Wave Packets Previous: Building a Localized Single-Particle Contents
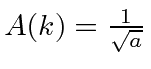 for
for
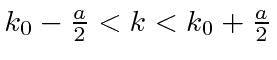 and 0 elsewhere.
and 0 elsewhere.
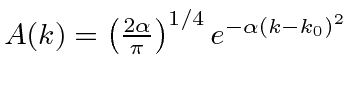 .
.
These are both localized in momentum about
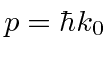 .
.
Check the normalization of (1).
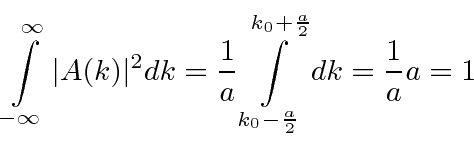
Check the normalization of (2) using the result for a
definite integral of a Gaussian
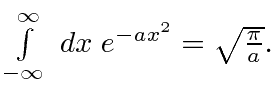
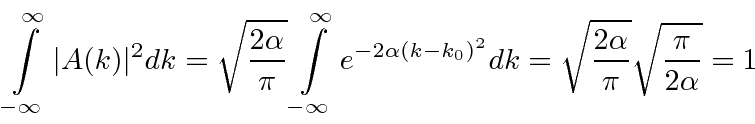
So now we take the Fourier Transform of (1) right here.
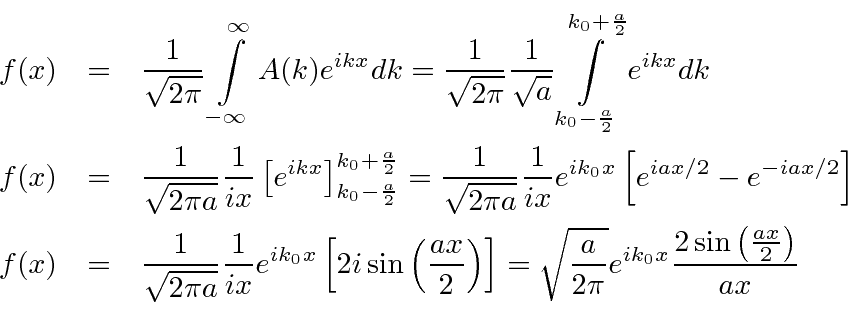
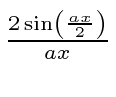 is equal to 1 at
is equal to 1 at
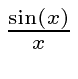 function.
function.
The
Fourier Transform of a Gaussian
wave packet
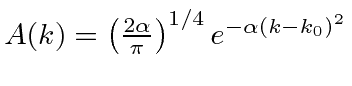 is
is
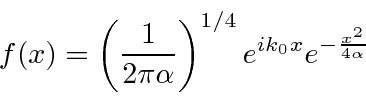
In both of these cases of
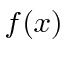 (transformed from a normalized
(transformed from a normalized
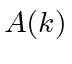 localized in momentum space) we see
localized in momentum space) we see
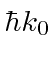 ,
,
We have achieved our goal of finding
states that represent one free particle.
We see that we can have states which are localized both in position space and momentum space.
We achieved this by making wave packets which are superpositions of states with definite momentum.
The wave packets, while localized, have some width in
![]() and in
and in
![]() .
.
Jim Branson 2013-04-22