Next: Operators Up: Course Summary Previous: Probability Amplitudes Contents
The probability amplitude for a free particle with momentum
![]() and energy
and energy
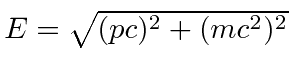 is the complex wave function
is the complex wave function
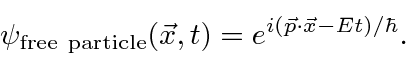
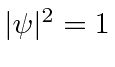 everywhere so this does not represent a localized particle.
In fact we recognize the wave property that, to have exactly one frequency,
a wave must be spread out over space.
everywhere so this does not represent a localized particle.
In fact we recognize the wave property that, to have exactly one frequency,
a wave must be spread out over space.
We can build up localized
wave packets that represent single particles
by adding up these free particle wave functions (with some coefficients).
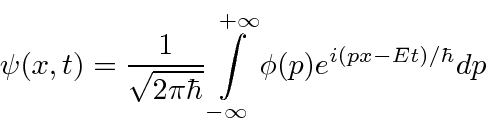
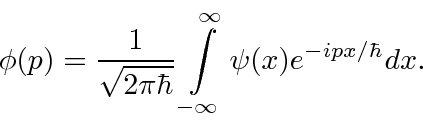
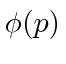 , are actually the state function of the particle in momentum space.
We can describe the state of a particle either in position space with
, are actually the state function of the particle in momentum space.
We can describe the state of a particle either in position space with
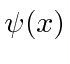 or in
momentum space with
or in
momentum space with
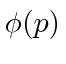 .
We can use
.
We can use
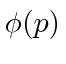 to compute the probability distribution function for momentum.
to compute the probability distribution function for momentum.
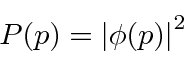
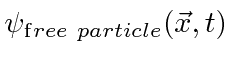 .
.
The Heisenberg
Uncertainty Principle
is a property of waves that we can deduce from our study of localized wave packets.
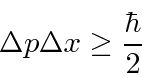
The next step in building up Quantum Mechanics is to determine how a wave function develops with time - particularly useful if a potential is applied. The differential equation which wave functions must satisfy is called the Schrödinger Equation.
Jim Branson 2013-04-22