Next: Examples Up: Diffraction Previous: Computing DeBroglie Wavelengths Contents
For our first thought experiment, we will consider two silt diffraction of light. Assume that instead of using the screen, I use a sensitive photo-detector. I measure the intensity of light as a function of position near the screen and find the same set of maxima and minima that I did using my eyes.
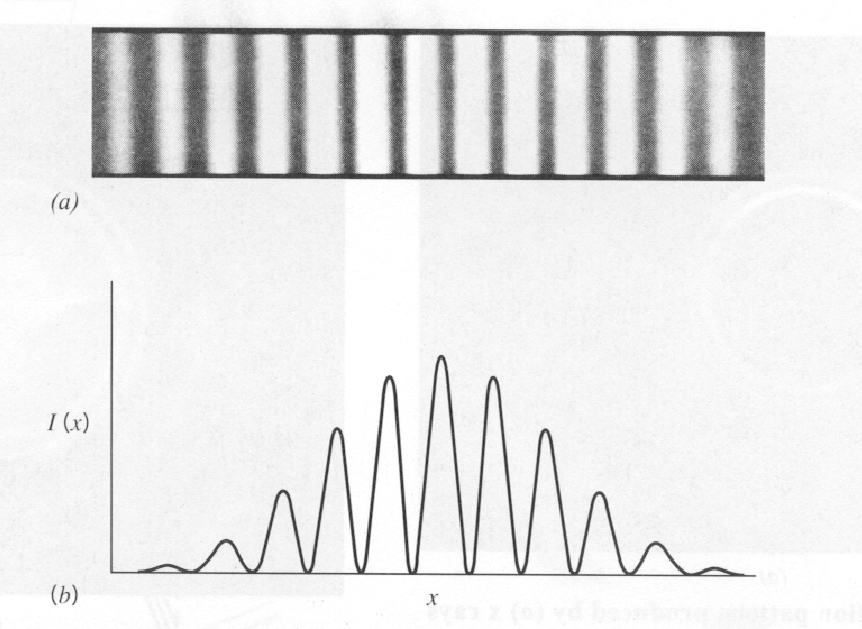
Now lets turn down the intensity of the light source.
For very low intensity I find that my detector collects
one photon at a time.
It never collects half a photon.
(With the right detector,
I could again verify that for each photon, the Photoelectric effect is seen and that
![]() .)
So the waves that are diffracting are somehow made up of photons.
With a low enough intensity, I can assure that only one photon is present in the apparatus at any time.
I can operate my detector and collect data over a long time, summing up the number of photons detected
as a function of position.
What will I get for the distribution?
I get exactly the same distribution as before with maxima and minima.
No matter how low the intensity, (1 particle/ minute!) we still see diffraction.
We never detect a fraction of an electron or a photon, only integer numbers.
.)
So the waves that are diffracting are somehow made up of photons.
With a low enough intensity, I can assure that only one photon is present in the apparatus at any time.
I can operate my detector and collect data over a long time, summing up the number of photons detected
as a function of position.
What will I get for the distribution?
I get exactly the same distribution as before with maxima and minima.
No matter how low the intensity, (1 particle/ minute!) we still see diffraction.
We never detect a fraction of an electron or a photon, only integer numbers.
How does a single photon interfere with itself? It must somehow travel through both slits.
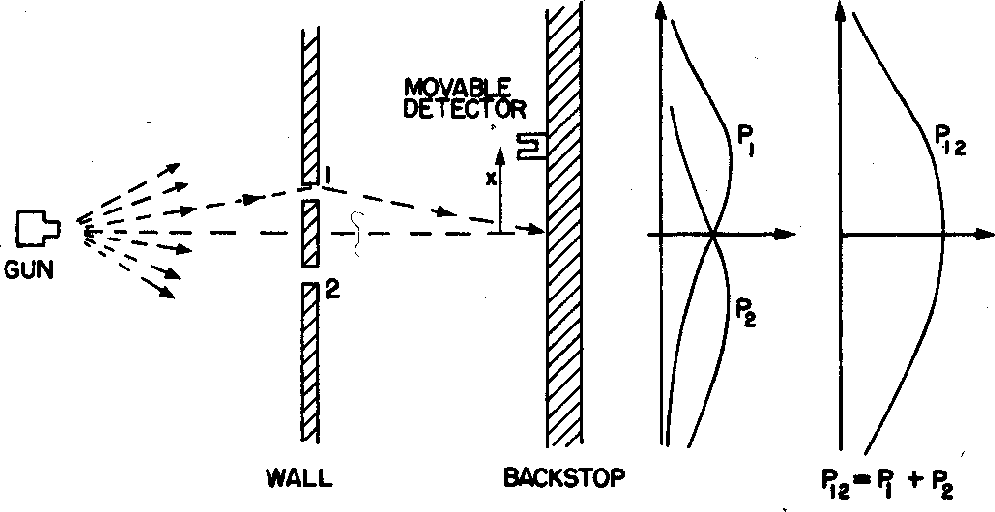
Lets turn to electron diffraction for a minute. In our thought experiment we again have two slits.
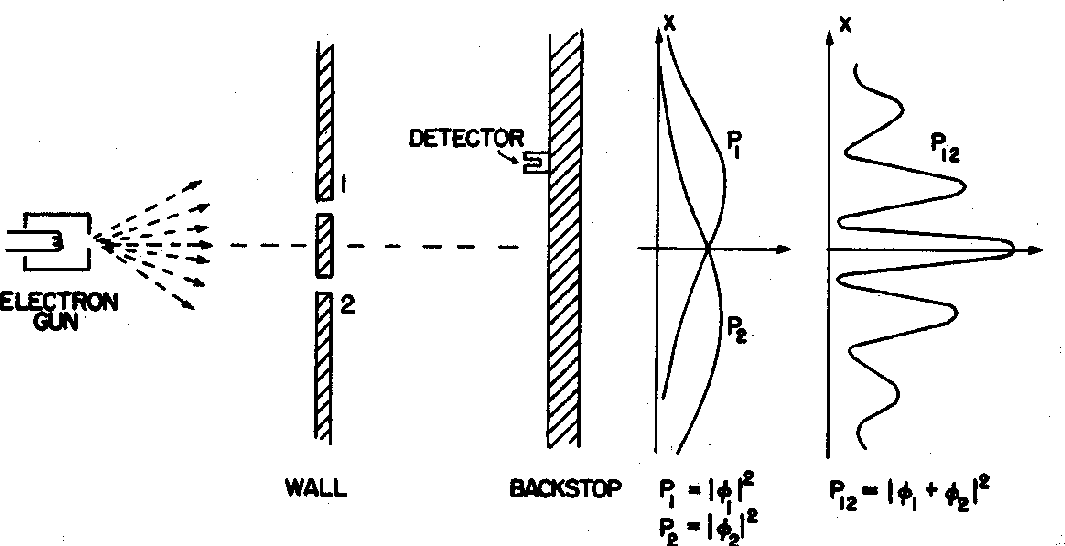
We use our detector to measure the diffraction pattern similar to the one for photons
labeled
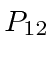 below.
If we cover up slit 2 we get the distribution labeled
below.
If we cover up slit 2 we get the distribution labeled
![]() and if we /emphtextcover up slit 1 we get the
intensity distribution labeled
and if we /emphtextcover up slit 1 we get the
intensity distribution labeled
![]() .
We could have done the same with our photons above.
.
We could have done the same with our photons above.
Now we will try to see which slit each electron passes through. We put a bright light source near the slits and detect light bouncing off the electron so we can see which slit it passes through.
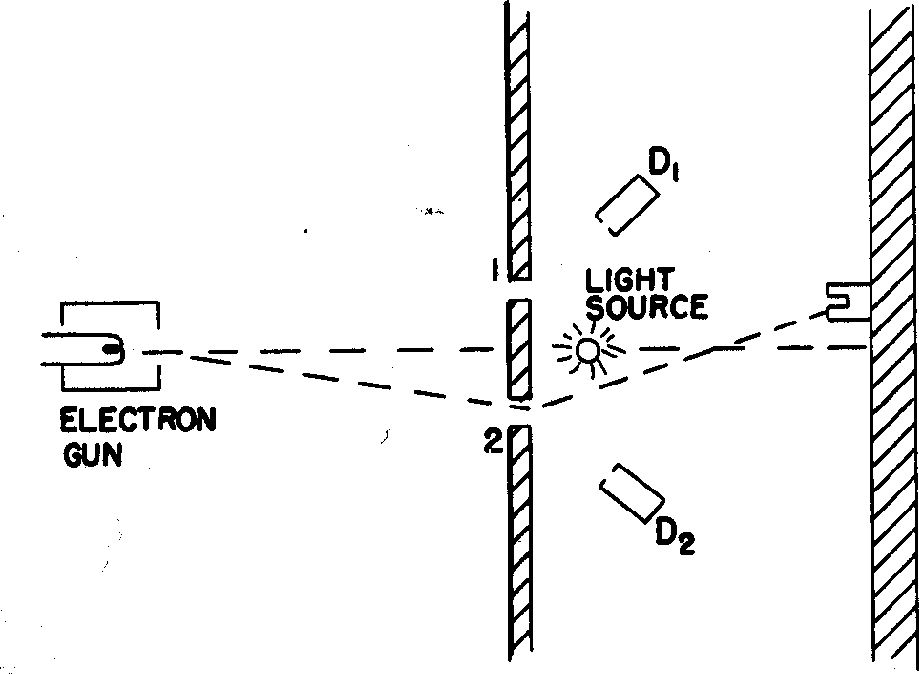
What distribution do we see now?
Actually we will see
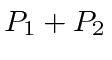 if we can tell which slit the electron went through.
Our observation of the electron as it passes through the slit has changed the resulting intensity distribution.
If we turn the light off, we go back to measuring
if we can tell which slit the electron went through.
Our observation of the electron as it passes through the slit has changed the resulting intensity distribution.
If we turn the light off, we go back to measuring
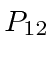 .
.
Can you explain why the light causes the diffraction pattern to disappear?
Is it the mere observation?
Does the light change the phase of the electron?
There are many examples of an observer changing the result of a Quantum experiment. Indeed, it is held that when a state is observed, its wave function collapses into the state ``seen''. In this case, all we had to do is turn on the light. We didn't have to look.
Finally, we will do a two slit diffraction experiment with bullets. We must make slits big enough for the bullets to pass through.
No matter what distance between the slits we choose, we never observe diffraction for the bullets.
They always give the
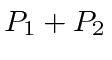 pattern (probably different for the bullets).
Can you explain this?
pattern (probably different for the bullets).
Can you explain this?
The bullet's wavelength is much much smaller than the actual size of the bullet.
Why didn't we see diffraction for the bullets.
Bullets are macroscopic objects with huge momenta compared to individual particles.
High momentum implies a small deBroglie wavelength.
So to see diffraction, we must make the distance between the slits much smaller than
we did for the photons (perhaps
![]() times smaller).
But bullets are also big.
They only fit through big slits which must them be further apart than the slits used for photons.
For bullets, the wavelength is tiny compared to any slit a bullet would fit through.
Therefore no bullet diffraction is possible.
times smaller).
But bullets are also big.
They only fit through big slits which must them be further apart than the slits used for photons.
For bullets, the wavelength is tiny compared to any slit a bullet would fit through.
Therefore no bullet diffraction is possible.
Feynman Lectures on Physics, Vol. III Chapter 1
Jim Branson 2013-04-22