The QED LaGrangian and Gauge Invariance

The LaGrangian for electrons, photons, and the interaction between the two is the LaGrangian of Quantum ElectroDynamics.

$$\bgroup\color{black}{\cal L}=-\hbar c\bar{\psi}\left(\gamma_\... ... 4}F_{\mu\nu}F_{\mu\nu}-ie\bar{\psi}\gamma_\mu A_\mu\psi\egroup$$

QED is our first complete example of an interacting Quantum Field Theory. It taught us a great deal about the laws of physics.

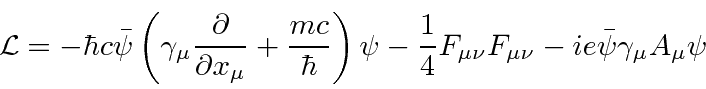
The primary difference between Quantum Mechanics and Quantum Field Theory is that particles can be created and destroyed. The probability to find an electron or a photon integrated over space does not have to be one. It can change with time. We have written the fields of the photon and the electron in terms of creation and annihilation operators.

$$\begin{eqnarray*} A_\mu &=&{1\over\sqrt{V}}\sum\limits_{k\alpha}\sqrt{\hbar c^2\... ...agger}_{\vec{p}} e^{i(\vec{p}\cdot\vec{x}-Et)/\hbar}\right) \\ \end{eqnarray*}$$

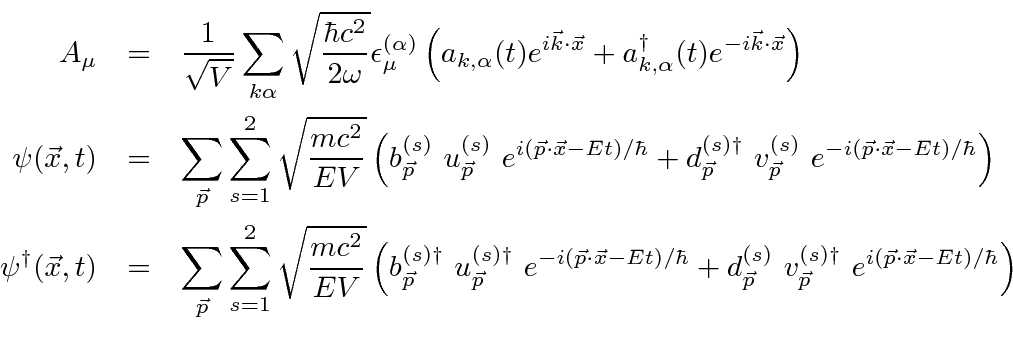
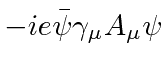Note that in the interaction term $-ie\bar{\psi}\gamma_\mu A_\mu\psi$ photons can be created or destroyed singly but that electrons must be created and destroyed along with a positron.

Phase (or Gauge) symmetry can be studied very simply from this LaGrangian. We have shown that the phase transformation

$$\begin{eqnarray*} \psi\rightarrow e^{i\lambda(x)}\psi \\ A_\mu\rightarrow A_\mu-{\hbar c\over e}{\partial\lambda(x)\over\partial x_\mu} \\ \end{eqnarray*}$$

leaves the Schrödinger equation invariant. This can be most directly studied using the LaGrangian. We can deduce from the above transformation that

$$\begin{eqnarray*} \bar{\psi}\rightarrow e^{-i\lambda(x)}\bar{\psi} \\ F_{\mu\nu... ...nu}{\partial\lambda(x)\over\partial x_\mu}\right)=F_{\mu\nu} \\ \end{eqnarray*}$$

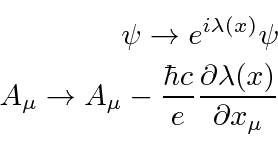
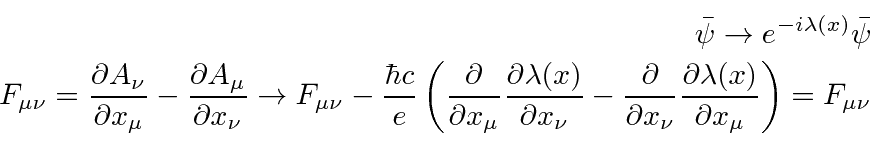
The transformed LaGrangian then can be computed easily.

$$\bgroup\color{black}{\cal L}=-\hbar c\bar{\psi}\left(\gamma_\... ... 4}F_{\mu\nu}F_{\mu\nu}-ie\bar{\psi}\gamma_\mu A_\mu\psi\egroup$$

The exponentials from $\bar{\psi}$ and $\psi$ cancel except for the term in which $\psi$ is differentiated.

$$\bgroup\color{black} {\cal L}\rightarrow{\cal L}-i\hbar c\bar... ...ver e}{\partial\lambda\over\partial x_\mu}\psi={\cal L} \egroup$$

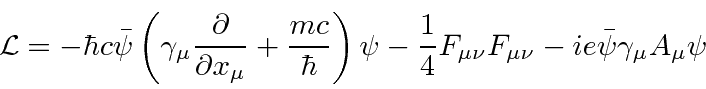
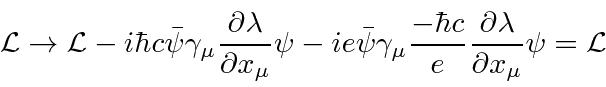
This all may seem fairly simple but imagine that we add a mass term for the EM field, 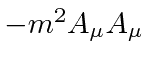$-m^2A_\mu A_\mu$. The LaGrangian is no longer gauge invariant. Gauge invariance implies zero mass photons and even maintains the massless photon after radiative corrections. Gauge invariance also implies the existence of a conserved current. Remember that electric current in 4D also includes the charge density. Gauge invariance implies conservation of charge, another important result.

This simple transformation 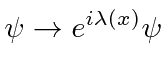$\psi\rightarrow e^{i\lambda(x)}\psi$ is called a local U(1) symmetry where the U stands for unitary.

The Weak interactions are based on an SU(2) symmetry. This is just a local phase symmetry times an arbitrary local rotation in SU(2) space. The SU(2) group is familiar to us since angular momentum is based on SU(2). In the weak interactions, there are two particles that are the symmetric (much like a spin up and a spin down electron but NOT a spin up and spin down electron). We can rotate our states into different linear combinations of the symmetric particles and the LaGrangian remains invariant. Given this local SU(2) symmetry of the fermion wave functions, we can easily deduce what boson fields are required to make the LaGrangian gauge invariant. It turns out we need a triplet of bosons. (The weak interactions then get messy because of the Higgs mechanism but the underlying gauge theory is still correct.)

The Strong interactions are based on the SU(3) group. Instead of having 3 sigma matrices to do rotations in the lowest dimension representation of the group, SU(3) has eight lambda matrices. The SU(3) symmetry for the quark wavefunctions requires an octet of massless vector boson called gluons to make the LaGrangian gauge invariant.

So the Standard Model is as simple as 1 2 3 in Quantum Field Theories.