In elastic scattering, the initial and final atomic states are the same, as are the initial and final photon energies.
With the help of some commutators, the 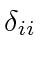 term can be combined with the others.
term can be combined with the others.
The commutator
![\bgroup\color{black}$[\vec{x},\vec{p}]$\egroup](img4066.png) (with no dot products) can be very useful in calculations.
When the two vectors are multiplied directly, we get something with two Cartesian indices.
(with no dot products) can be very useful in calculations.
When the two vectors are multiplied directly, we get something with two Cartesian indices.
The commutator of the vectors is
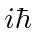 times the identity.
This can be used to cast the first term above into something like the other two.
times the identity.
This can be used to cast the first term above into something like the other two.
Now we need to put the states in using an identity, then use the commutator with
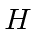 to change
to change
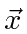 to
to
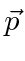 .
.
(Reminder:
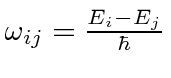 is just a number.
is just a number.
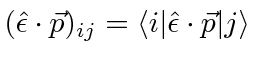 is a matrix element between states.)
is a matrix element between states.)
We may now combine the terms for elastic scattering.
This is a nice symmetric form for elastic scattering.
If computation of the matrix elements is planned, it useful to again use the commutator to change
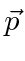 into
into
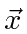 .
.
Jim Branson
2013-04-22
![\begin{displaymath}\bgroup\color{black} {d\sigma_{elastic}\over d\Omega}
= \left...
...rangle
\over \omega_{ji}+\omega}
\right] \right\vert^2 \egroup\end{displaymath}](img4064.png)
![\bgroup\color{black}$[\vec{x},\vec{p}]$\egroup](img4066.png) (with no dot products) can be very useful in calculations.
When the two vectors are multiplied directly, we get something with two Cartesian indices.
(with no dot products) can be very useful in calculations.
When the two vectors are multiplied directly, we get something with two Cartesian indices.
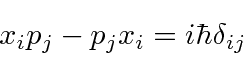
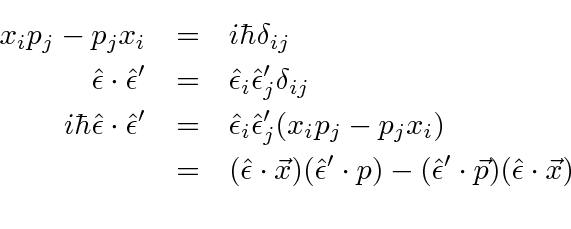
![\begin{eqnarray*}
1&=&\sum\limits_j\langle i\vert j\rangle \langle j\vert i\ran...
...}\cdot\vec{p})_{ij}(\hat{\epsilon}'\cdot\vec{p})_{ji}\right] \\
\end{eqnarray*}](img4070.png)
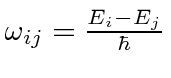 is just a number.
is just a number.
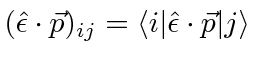 is a matrix element between states.)
is a matrix element between states.)
![\begin{eqnarray*}
{d\sigma_{elas}\over d\Omega}
&=&\left({e^2\over 4\pi mc^2}\ri...
...\over \omega_{ji}(\omega_{ji}+\omega)}
\right] \right\vert^2 \\
\end{eqnarray*}](img4073.png)
![\bgroup\color{black}$\displaystyle
{d\sigma_{elas}\over d\Omega}
=\left({e^2\ov...
...\vec{x} \vert i\rangle
\over \omega_{ji}+\omega}
\right] \right\vert^2
$\egroup](img4074.png)