Next: Fourier Decomposition of Radiation Up: Quantum Theory of Radiation Previous: Quantum Theory of Radiation Contents
In non-relativistic Quantum Mechanics, the static Electric field is represented by a scalar potential,
magnetic fields by the vector potential, and the radiation field also through the vector potential.
It will be convenient to keep this separation between the large static atomic Electric field and the
radiation fields, however, the equations we have contain the four-vector
![]() with all the fields mixed.
When we quantize the field,
all E and B fields as well as electromagnetic waves will be made up of photons.
It is useful to be able to
separate the E fields due to fixed charges from the EM radiation from moving charges.
This separation is not Lorentz invariant, but it is still useful.
with all the fields mixed.
When we quantize the field,
all E and B fields as well as electromagnetic waves will be made up of photons.
It is useful to be able to
separate the E fields due to fixed charges from the EM radiation from moving charges.
This separation is not Lorentz invariant, but it is still useful.
Enrico Fermi showed, in 1930, that
![]() together with
together with
![]() give rise to Coulomb interactions between particles,
whereas
give rise to Coulomb interactions between particles,
whereas
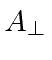 gives rise to the EM radiation from moving charges.
With this separation, we can maintain the form of our non-relativistic Hamiltonian,
gives rise to the EM radiation from moving charges.
With this separation, we can maintain the form of our non-relativistic Hamiltonian,
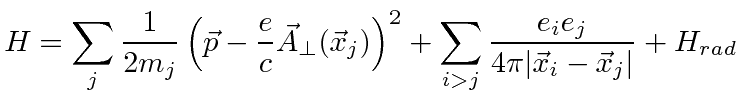 |
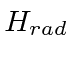 is purely the Hamiltonian of the radiation (containing only
is purely the Hamiltonian of the radiation (containing only
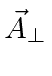 ),
and
),
and
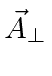 is the part of the vector potential which satisfies
is the part of the vector potential which satisfies
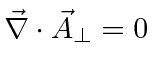 .
Note that
.
Note that
In a region in which there are no source terms,
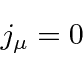
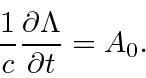
If
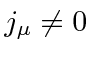 , then we cannot eliminate
, then we cannot eliminate
![]() ,
since
,
since
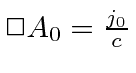 and we are only allowed to make gauge transformations for which
and we are only allowed to make gauge transformations for which
![]() .
In this case we must separate the vector potential into the transverse and longitudinal parts, with
.
In this case we must separate the vector potential into the transverse and longitudinal parts, with
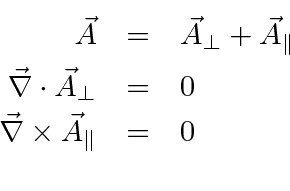
We will now study the radiation field in a region with no sources so that
![]() .
We will use the equations
.
We will use the equations
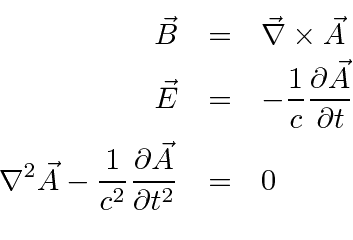
Jim Branson 2013-04-22