Next: Hund's Rules Up: Atomic Physics Previous: Atomic Shell Model Contents
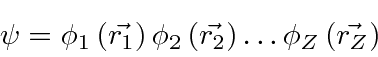
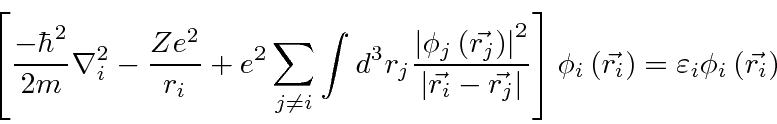
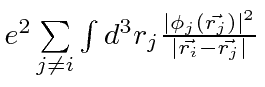 represents the potential due to the other electrons
in which electron
represents the potential due to the other electrons
in which electron
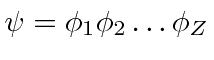 .
Since we will not apply these equations to solve problems, we will not go into the
derivation, however, it is useful to know how one might proceed to solve more difficult problems.
.
Since we will not apply these equations to solve problems, we will not go into the
derivation, however, it is useful to know how one might proceed to solve more difficult problems.
An improved formalism known as the Hartree-Fock equations, accounts for the required antisymmetry and gives slightly different results.
Jim Branson 2013-04-22