Next: Hyperfine and Zeeman for Up: Examples Previous: Intermediate Field Contents
Positronium, the Hydrogen-like bound state of an electron and a positron, has a ``hyperfine'' correction which is as large as the fine structure corrections since the magnetic moment of the positron is the same size as that of the electron. It is also an interesting laboratory for the study of Quantum Physics. The two particles bound together are symmetric in mass and all other properties. Positronium can decay by anihilation into two or more photons.
In analyzing positronium, we must take some care to correctly handle the relativistic correction in the case of a reduced mass much different from the electron mass and to correctly handle the large magnetic moment of the positron.
The zero order energy of positronium states is
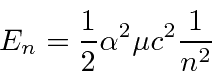
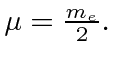
The relativistic correction must take account of both the motion of the electron and
the positron.
We use
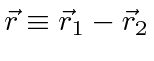 and
and
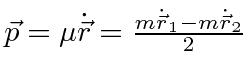 .
Since the electron and positron are of equal mass, they are always exactly
oposite each other in the center of mass and so the momentum vector we use is
easily related to an individual momentum.
.
Since the electron and positron are of equal mass, they are always exactly
oposite each other in the center of mass and so the momentum vector we use is
easily related to an individual momentum.
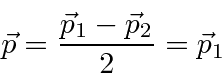
We will add the relativistic correction for both the electron
and the positron.
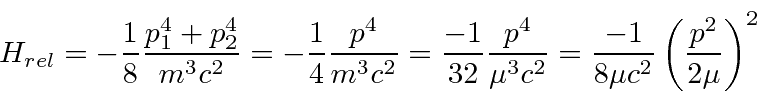
The spin-orbit correction should be checked also.
We had
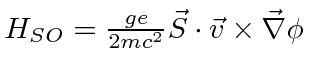 as the interaction
between the spin and the B field producded by the orbital motion.
Since
as the interaction
between the spin and the B field producded by the orbital motion.
Since
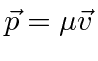 , we have
, we have
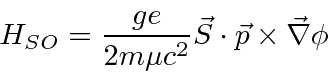
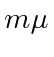 in the
denominator.
The final formula then is
in the
denominator.
The final formula then is
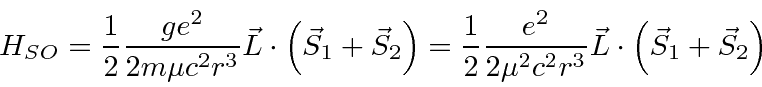
The calculation of the spin-spin (or hyperfine) term also needs some attention.
We had
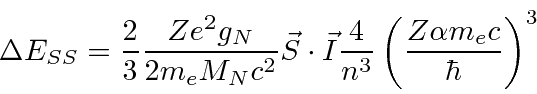
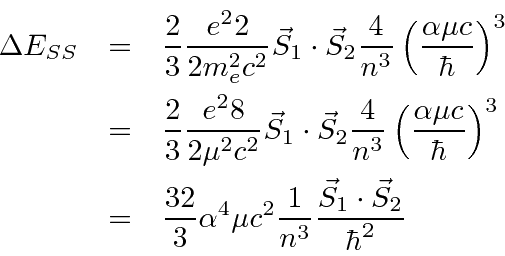
Jim Branson 2013-04-22