Splitting of the Hydrogen Ground State

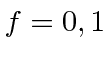The ground state of Hydrogen has a spin $\bgroup\color{black}$1\over2$\egroup$ electron coupled to a spin $\bgroup\color{black}$1\over2$\egroup$ proton, giving total angular momentum state of $\bgroup\color{black}$ f=0,1 $\egroup$ . We have computed in first order perturbation theory that

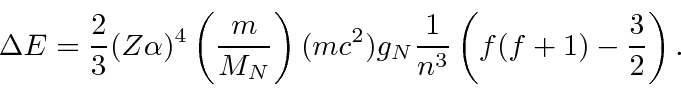
$\begin{displaymath}\bgroup\color{black} \Delta E = {2\over 3} (Z\alpha)^4 \left(... ...mc^2) g_N {1\over{n^3}} \left(f(f+1)-{3\over 2}\right). \egroup\end{displaymath}$

The energy difference between the two hyperfine levels determines the wave length of the radiation emitted in hyperfine transitions.

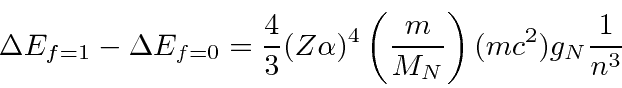
$\begin{displaymath}\bgroup\color{black} \Delta E_{f=1} - \Delta E_{f=0} = {4\ove... ...^4 \left({m\over{M_N}}\right) (mc^2) g_N {1\over{n^3}} \egroup\end{displaymath}$

For $\bgroup\color{black}$n=1$\egroup$ Hydrogen, this gives

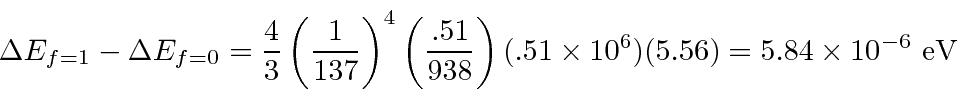
$\begin{displaymath}\bgroup\color{black} \Delta E_{f=1} - \Delta E_{f=0} = {4\ov... ...t) (.51\times 10^6)(5.56)=5.84\times 10^{-6}\mbox{ eV} \egroup\end{displaymath}$

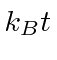Recall that at room temperature, $\bgroup\color{black}$k_Bt$\egroup$ is about $\bgroup\color{black}${1\over 40}$\egroup$ eV, so the states have about equal population at room temperature. Even at a few degrees Kelvin, the upper state is populated so that transitions are possible. The wavelength is well known.

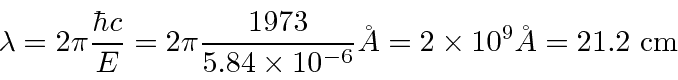
$\begin{displaymath}\bgroup\color{black}\lambda = 2\pi{\hbar c\over E} = 2\pi{197... ...imes 10^{-6}}}\AA = 2\times 10^9 \AA = 21.2\mbox{ cm} \egroup\end{displaymath}$

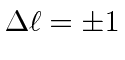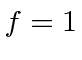This transition is seen in interstellar gas. The $\bgroup\color{black}$f=1$\egroup$ state is excited by collisions. Electromagnetic transitions are slow because of the selection rule $\bgroup\color{black}$\Delta\ell=\pm 1$\egroup$ we will learn later, and because of the small energy difference. The $\bgroup\color{black}$f=1$\egroup$ state does emit a photon to de-excite and those photons have a long mean free path in the gas.

Jim Branson 2013-04-22